标签:
开始的地方先放上关于二叉树的定义
二叉树:
是n(n>=0)个结点的有限集合,它或者是空树(n=0),或者是由一个根结点及两颗互不相交的、分别称为左子树和右子树的二叉树所组成。
满二叉树:
一颗深度为k且有2^k-1个结点的二叉树称为满二叉树。
除叶子结点外的所有结点均有两个子结点。节点数达到最大值。所有叶子结点必须在同一层上。
完全二叉树:
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
例:
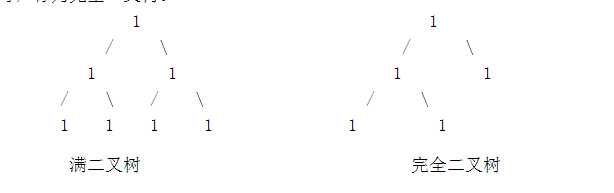
假设所有的二叉树的结构为
typedef struct BinaryTreNode { int NodeValue; BinaryTreNode *lchild, *rchild; }BitNode;
一、二叉树的简单遍历有三种:前序遍历、中序遍历和后续遍历,其实现方法如下:
1 void PreOrder(BitNode *parent) 2 { 3 if (parent!=NULL) 4 { 5 printf("%d\t",parent->NodeValue); 6 PreOrder(parent->lchild); 7 PreOrder(parent->rchild); 8 } 9 } 10 void InOrder(BitNode *parent) 11 { 12 if (parent != NULL) 13 { 14 InOrder(parent->lchild); 15 printf("%d\t", parent->NodeValue); 16 InOrder(parent->rchild); 17 } 18 } 19 void PostOrder(BitNode *parent) 20 { 21 if (parent!=NULL) 22 { 23 PostOrder(parent->lchild); 24 PostOrder(parent->rchild); 25 printf("%d\t", parent->NodeValue); 26 } 27 }
二、根据二叉树的前序遍历和中序遍历打印出二叉树
代码如下:
1 BinaryTreNode* ConstructCore(int *StartPreorder,int *EndPreorder,int *StartInorder,int *EndInorder) 2 { 3 //前序遍历序列的第一个数字是根节点的值 4 int rootvalue = StartPreorder[0]; 5 BinaryTreNode *root = new BinaryTreNode(); 6 root->NodeValue = rootvalue; 7 if (StartPreorder==EndPreorder) 8 { 9 if (StartInorder == EndInorder && *StartPreorder == *StartInorder) 10 return root; 11 else 12 throw std::exception("Invalid input."); 13 } 14 //在中序遍历序列中找到根节点的值 15 int *rootInorder = StartInorder; 16 while (*rootInorder != rootvalue&&rootInorder <= EndInorder) 17 ++rootInorder; 18 if (rootInorder == EndInorder&&*rootInorder != rootvalue) 19 throw std::exception("Invalid input."); 20 int LeftLength = rootInorder - StartInorder; 21 int *LeftEndOrder = StartPreorder + LeftLength; 22 if (LeftLength>0) 23 { 24 //构建左子树 25 root->lchild = ConstructCore(StartPreorder,LeftEndOrder,StartInorder,rootInorder-1); 26 } 27 if (LeftLength<EndPreorder-StartPreorder) 28 { 29 //构建右子树 30 root->rchild = ConstructCore(LeftEndOrder+1,EndPreorder,rootInorder+1,EndInorder); 31 } 32 return root; 33 } 34 BinaryTreNode* Construct(int *preorder, int *inorder, int length) 35 { 36 if (preorder == NULL || inorder == NULL || length <= 0) 37 return NULL; 38 39 return ConstructCore(preorder, preorder + length - 1, inorder, inorder + length - 1); 40 }
算法的核心是找到根节点,然后根据根节点和位置和中序遍历确定左子树的结点个数和右子树的结点个数,进行递归计算,从而打印出二叉树。
标签:
原文地址:http://www.cnblogs.com/jingliming/p/4450781.html