标签:
AVL树为了防止树的深度过深出现的一种数据结构,在二叉树的基础上添加了一条规则:每个节点的左子数与右子树的高度最多差1。
其中的难点之一为:插入一个节点。删除一个节点更难,在这里采用懒惰删除法。其中,在插入的时候更新根节点路径上那些节点的所有高度。
AVL节点:
struct AvlNode { ElementType Element; AvlTree Left; AvlTree Right; int Height; };
//问题一:当插入一个节点时,如何知道哪个节点失去平衡
在插入一个节点的时候,可以通过对树进行简单的修正来使新的树满足AVL树的特性----旋转。
把需要平衡的节点叫做a。由于任意节点最多有两个节点,因此高度不平衡时,a点的两棵子树的高度差2。可以猜想出,这种不平衡可能出现在下列四种情况中:
其中情形1和3,2和4是关于a点镜像对称,具体巧妙可在代码中看出。其中调整1和3的情况是进行一次单旋转,2和4则需要一次双旋转。
1.对a的左儿子的左子树进行一次插入时,出现不平衡的情形为:
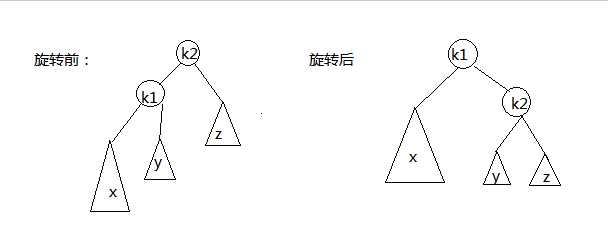
旋转代码为:
static Position SingleRotateWithLeft(Position K2) { Position K1; K1 = K2->Left; K2->Left = K1->Right; K1->Right = K2; K2->Height = Max(Height(K2->Left), Height(K2->Right)) + 1; K1->Height = Max(K2->Height, Height(K1->Right)) + 1; return K1; }
2.对a的左儿子的右子树插入一个节点,出现不平衡的情形为: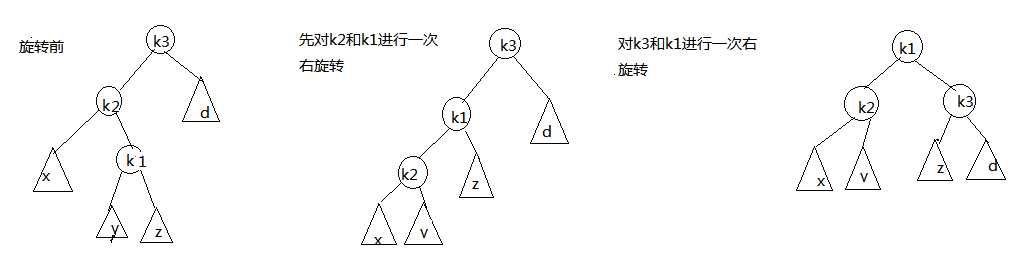
旋转代码为:
static Position DoubleRotateWithLeft(Position K3) { K3->Left = SingleRotateWithRight(K3->Left); return SingleRotateWithLeft(K3); }
3和4的旋转代码为:
static Position SingleRotateWithRight(Position K2) { Position K1; K1 = K2->Right; K2->Right = K1->Left; K1->Left = K2; K2->Height = Max(Height(K2->Left), Height(K2->Right)) + 1; K1->Height = Max(K2->Height, Height(K1->Right)) + 1; return K1; } static Position DoubleRotateWithRight(Position K3) { K3->Right = SingleRotateWithLeft(K3->Right); return SingleRotateWithRight(K3); }
标签:
原文地址:http://www.cnblogs.com/dd550023981/p/4458603.html