标签:
1.引言
卷积神经网络(Convolutional Neural Networks , CNN)受到视网膜上的细胞只对视野范围内的部分区域敏感,这一部分区域称为感受域(receptive field).卷积神经网络正是采用了这种机制,每一个神经元只与一部分输入相连接。
2.稀疏连接
CNNs通过局部连接的方式揭示了空间中的局部相关性。在 $m$ 层的隐单元的输入来自于 $m-1$ 层的一部分单元的加权和,这一部分单元在空间上是连续的感受域。如下图:
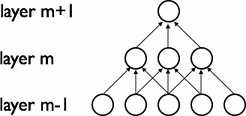
可以把 $m-1$ 层想象成视网膜输入。$m$ 层的单元的感受域的宽度均为3,因此只与视网膜层的 3 个相邻的神经元相连接。$m+1$ 层的单元与其下面一层的连接方式也是如此。每一个神经元对不在感受域范围内的变化是没有反应的,所以上面的结构保证学习出一种“滤波器“,使其对局部空间的输入模式产生强烈的反应。
但是,正如上面图中所示,把许多这样的滤波器层层级联,局部感知逐渐变得全局感知,$m$ 层的每一个单元只对部分输入感知,而 $m+1$ 层的单元又将 $m$ 层的感知结果综合起来从而形成对输入层全部的一个感知,所以$m+1$隐层单元可以看作是对宽度为5的特征的一个非线性编码。
3.共享权重(Shared Weights)
在CNNs,每个滤波器 $h_{i}$ 重复地逐步横跨整个输入层。重复的单元共享参数(权重向量和偏置),从而形成一幅特征图。
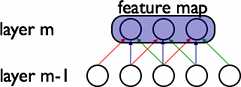
在上图中,3个隐层单元属于同一幅特征图,一样颜色的权重值是共享的,即相等的。
滤波器通过这种方式使得图像中可视层中任意位置的特征都能被检测出来,权重共享大大减少了需要学习的参数的数量。
4.细节和符号
通过重复地把一个函数运用到整个图像的子区域可以得到一幅特征图,即用一个线性滤波器对图像进行卷积操作,加上偏置项,然后再采用一个非线性函数。如果用 $h^{k}$ 表示第 $k$ 层的特征图,其对应的滤波器由 $W^{k}$ 和偏置 $b_{k}$ 决定, 那么特征图 $h^{k}$ 可以由下计算得到(采用 tanh 进行非线性函数):
$h_{ij}^{k}=tanh((W^{k}*x)_{ij}+b_{k}$
为了得到对数据更加丰富的表示,通常每个隐层都由多幅特征图组成:$\{h^{\text{(k)}},k=0,...K\}$.权重 $W$ 由一个4维的张量表示, 4各维度分别表示:目的特征图,源特征图,源特征图的垂直坐标,源特征图的水平坐标。偏置 $b$ 由一个向量表示,其中每一个元素是每一个目标特征图对应的偏置。可以表示如下:
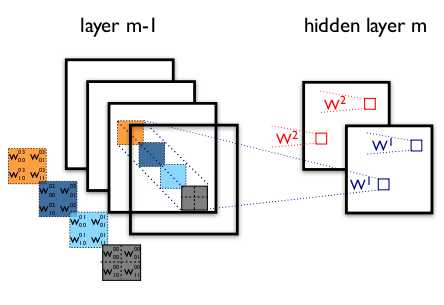
在上图中 $W_{ij}^{kl}$ 表示在 $m-1$ 层的第 $k$ 幅特征图的每一个像素 与第 $m$ 层的第 $l$ 幅特征图的像素 $(i,j)$ 之间的连接权重。
标签:
原文地址:http://www.cnblogs.com/90zeng/p/4461876.html