标签:
斐波那契堆是一个可合并最小堆,提取最小节点和删除节点的时间复杂度为o(logn),其他操作的平摊时间复杂度为o(1)
表示方式:
斐波那契堆以一个树结构表示,父节点有一个度数表示有几个子节点,同时保存指向自身的一个子节点的指针,子节点通过left和right形成一个循环链表连接所有同级节点
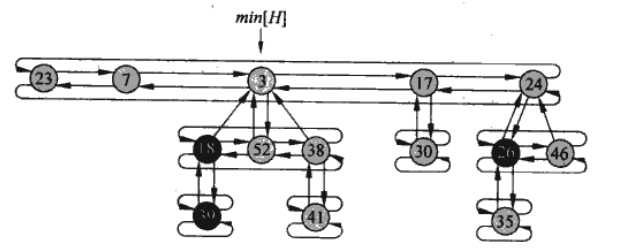
如上图所示,借用算法导论的示例图,堆中只保存一个指向最小节点的指针
static class Node { int key; String value; Node parent; Node child; Node left; Node right; int degree = 0; boolean mark = false; public Node(int key, String value) { this.key = key; this.value = value; this.left = this; this.right = this; } public String toString() { return String.format("key: %d, value: %s, degree: %d", key, value, degree); } }
主要操作:
可以支持最小堆的合并、提取最小值、删除节点、减小节点key,插入新节点等操作;
合并操作很简单,就是把两个堆的根节点链表连起来,同时比较两个堆的最小节点,重新找出最小节点;
将新node插入根节点链表,同时与最小值比较,找出最小节点(插入节点也可以看做是与一个只有一个节点的堆合并);
只需返回min的节点即可;
这个是其中最复杂的操作,可以分以下几步:
1)找到最小的根节点并删除它,将所有的子节点都加入堆的根表;
2)合并相同度数的节点:建立以节点的度数为下标的数组,遍历根节点,如果数组中有数据则合并,没有数据则插入,确保相同度数的节点只有一个;
3)重新找出最小节点
1)与父节点比较,如果新的key仍然大于父节点的key,直接return;
2)如果小于父节点,添加到根节点链表中;
3)与min节点比较,重新选择最小节点;
删除节点是减小节点和提取最小节点的混合操作,先把要删除节点的key减小至最小,然后删除min节点
package com.feinno.algorithmic.heap; import java.util.LinkedList; import java.util.List; import java.util.Random; /** * 最小合并堆,斐波那契堆 * * @author renzhaolong * * @param <K> * @param <V> */ public class FibonacciHeap { private Node min; private int nodeCount; private int potential; /** * 添加新节点 1. 添加到min的同级节点 2. 如果min大于新节点,将min指为新节点 * * @param key * @param value * @return */ public Node add(Node newNode) { if (null == newNode) { throw new NullPointerException("node could not be null"); } if (null == min) { min = newNode; } else { addHorizontal(min, newNode); if (bigger(min, newNode)) { min = newNode; } } nodeCount++; return newNode; } /** * 获取最小节点 * * @return */ public Node getMin() { return min; } /** * 分为三步: * 1)找到最小的根节点并删除它,将所有的子节点都加入堆的根表; * 2)合并相同度数的节点:建立以节点的度数为下标的数组,遍历根节点, * 如果数组中有数据则合并,没有数据则插入,确保相同度数的节点只有一个; * 3)重新找出最小节点 * * @return */ public Node extractmin() { if (null == min) return null; Node result = min; addAllToRoot(result.child); delMin(); consolidateHeap(); return result; } /** * 将一个堆合并到当前堆 * 合并根节点链表 * * @param heap */ public void mergeHeap(FibonacciHeap heap) { nodeCount += heap.nodeCount; potential += heap.potential; addAllToRoot(heap.min); if (bigger(min, heap.min)) { min = heap.min; } } /** * 减小堆中的node * * @param node * @param newKey */ public void decreaseNode(Node node, int newKey) { doDecreaseNode(node, newKey); } /** * 删除节点 * * @param node */ public void delNode(Node node) { doDecreaseNode(node, Integer.MIN_VALUE); extractmin(); } /** * * 如果新的key仍然大于父节点的key,直接return;如果小于父节点,添加到根节点链表中; * * @param node * @param newKey */ private void doDecreaseNode(Node node, int newKey) { node.key = newKey; if (bigger(node.parent, node)) { addNodeToRoot(node); } if (bigger(min, node)) { min = node; } } private void addNodeToRoot(Node node) { Node parent = node.parent; if (null == parent) { return; } node.parent = null; parent.degree--; addHorizontal(min, node); if (!parent.mark) { parent.mark = true; potential++; } else { addNodeToRoot(parent); } } private int getArrLen() { return (int) Math.ceil(Math.log(nodeCount + potential) / Math.log(2)) + 1; } /** * 压缩堆的根节点,遍历root,发现度数相同的合并之 */ private void consolidateHeap() { if (null == min) { return; } Node current = null; Node next = min.right; Node[] degreeArr = new Node[getArrLen()]; List<Node> allroot = new LinkedList<Node>(); allroot.add(min); while (min != next) { allroot.add(next); next = next.right; } for (int i = 0; i < allroot.size(); i++) { current = allroot.get(i); while (true) { if (null == degreeArr[current.degree]) { degreeArr[current.degree] = current; break; } Node temp = degreeArr[current.degree]; degreeArr[current.degree] = null; current = mergeNode(temp, current); } } for (int i = 0; i < degreeArr.length; i++) { if (null == degreeArr[i]) { continue; } Node temp = (Node) degreeArr[i]; if (bigger(min, temp)) { min = temp; } } } /** * 合并两个根节点,返回合并后的节点 * * @param node1 * @param node2 * @return */ private Node mergeNode(Node node1, Node node2) { // 使node1为较小节点 if (bigger(node1, node2)) { Node temp = node1; node1 = node2; node2 = temp; } // 将node2从根节点删除 node2.left.right = node2.right; node2.right.left = node2.left; // 将node2加入node1根节点 node2.parent = node1; if (null == node1.child) { node1.child = node2; node2.left = node2; node2.right = node2; } else { addHorizontal(node1.child, node2); } node1.degree++; return node1; } private void delMin() { if (min.right == min) { min = null; } else { min.left.right = min.right; min.right.left = min.left; min = min.right; } nodeCount--; } private boolean bigger(int key1, int key2) { return (long) key1 - key2 > 0; } private boolean bigger(Node node1, Node node2) { return bigger(node1.key, node2.key); } /** * 将节点的同级全部加到root * * @param node */ private void addAllToRoot(Node node) { if (null == node) { return; } node.parent = null; Node next = node; while (node != next.right) { next = next.right; next.parent = null; } next.right = min.right; next.right.left = next; min.right = node; node.left = min; } /** * 添加一个同级节点 * * @param node * @param newNode */ private void addHorizontal(Node node, Node newNode) { newNode.right = node.right; newNode.right.left = newNode; newNode.left = node; node.right = newNode; } private int checkCount = 0; public boolean check() { checkCount = 0; if (false == checkNode(min, min)) { return false; } return checkCount == nodeCount; } private boolean checkNode(Node beginNode, Node node) { if (node == null) return true; checkCount++; if (bigger(min, node)) return false; Node next = node.right; if (next != beginNode) { if (false == checkNode(beginNode, next)) { return false; } } return checkNode(node.child, node.child); } public static void main(String[] args) { FibonacciHeap heap = new FibonacciHeap(); List<Node> adds = new LinkedList<Node>(); Random ran = new Random(); for (int i = 0; i < 1000; i++) { int key = ran.nextInt(10000000); Node node = new Node(key, ""); adds.add(node); heap.add(node); if (false == heap.check()) { System.out.println("error:" + node); } else { System.out.println("ok:" + node); } } for (int i = 0; i < 1000; i++) { Node min = heap.extractmin(); if (false == heap.check()) { System.out.println("error: " + min); heap.check(); } } } static class Node { int key; String value; Node parent; Node child; Node left; Node right; int degree = 0; boolean mark = false; public Node(int key, String value) { this.key = key; this.value = value; this.left = this; this.right = this; } public String toString() { return String.format("key: %d, value: %s, degree: %d", key, value, degree); } } }
标签:
原文地址:http://www.cnblogs.com/remagon/p/4462561.html