POJ_2446_Chessboard(二分图匹配)

标签：algorithm   acm   poj   二分图   匈牙利算法   

Description

Alice and Bob often play games on chessboard. One day, Alice draws a board with size M * N. She wants Bob to use a lot of cards with size 1 * 2 to cover the board. However, she thinks it too easy to bob, so she makes some holes on the board (as shown in the figure below).

We call a grid, which doesn’t contain a hole, a normal grid. Bob has to follow the rules below:
1. Any normal grid should be covered with exactly one card.
2. One card should cover exactly 2 normal adjacent grids.

Some examples are given in the figures below:

A VALID solution.

An invalid solution, because the hole of red color is covered with a card.

An invalid solution, because there exists a grid, which is not covered.
Your task is to help Bob to decide whether or not the chessboard can be covered according to the rules above.

Input

Output

Sample Input

4 3 2
2 1
3 3

Sample Output

YES

Hint

A possible solution for the sample input.

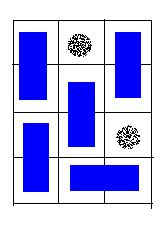
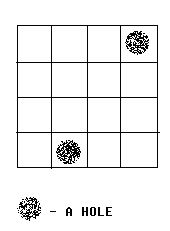
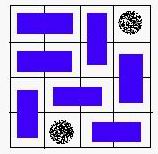
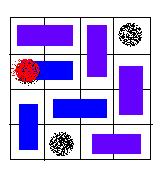
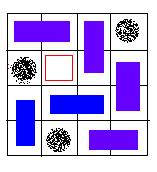
题意：给出一个矩形N*M棋盘，有K个格子是空洞，然后用2*1的矩形，对所有非空洞的格子进行覆盖，问能否完全覆盖。

分析：二分图匹配问题。关键问题是如何建图，我们可以把每两个相邻的非空格子用一条边连接起来，这样的话相当于这两个格子处于分别处于两个集合当中，这样的话两个相邻的格子就不会处于同一个集合当中。然后这样子连边就构成了一个二分图了。然后求出最大匹配数。如果匹配数 + k = N*M，输出“YES”。

题目链接：http://poj.org/problem?id=2446

代码清单：

#include<map>
#include<queue>
#include<cmath>
#include<stack>
#include<ctime>
#include<cctype>
#include<string>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn = 32 + 5;
const int maxv = 2000 + 5;

int m,n,k;
int x,y,cnt;

int match[maxv];
bool vis[maxv];
int num[maxn][maxn];
bool hole[maxn][maxn];
bool graph[maxv][maxv];

bool dfs(int u){         //匈牙利算法
    for(int v=1;v<=cnt;v++){
        if(!vis[v]&&graph[u][v]){
            vis[v]=true;
            if(match[v]==-1 || dfs(match[v])){
                match[v]=u;
                return true;
            }
        }
    }return false;
}

bool ok(){
    int ans=0;
    for(int i=1;i<=cnt;i++){
        memset(vis,false,sizeof(vis));
        if(dfs(i)) ans++;
    }
    if(ans==cnt) return true;
    return false;
}

int main(){
    scanf("%d%d%d",&m,&n,&k);
    memset(match,-1,sizeof(match));
    memset(hole,false,sizeof(hole));
    memset(graph,false,sizeof(graph));
    for(int i=0;i<k;i++){
        scanf("%d%d",&x,&y);
        hole[y-1][x-1]=true;
    }
    if((n*m-k)&1) printf("NO\n"); //奇偶性剪枝

    else{
        cnt=0;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(!hole[i][j])
                    num[i][j]=++cnt;
            }
        }

        //建立二分图
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(!hole[i][j]){  
                    if(i-1>=0&&!hole[i-1][j]) graph[num[i][j]][num[i-1][j]]=true;
                    if(i+1<m&&!hole[i+1][j]) graph[num[i][j]][num[i+1][j]]=true;
                    if(j-1>=0&&!hole[i][j-1]) graph[num[i][j]][num[i][j-1]]=true;
                    if(j+1<n&&!hole[i][j+1]) graph[num[i][j]][num[i][j+1]]=true;
                }
            }
        }

        if(ok()) printf("YES\n");
        else printf("NO\n");
    }
    return 0;
}

POJ_2446_Chessboard(二分图匹配)

标签：algorithm   acm   poj   二分图   匈牙利算法   

原文地址：http://blog.csdn.net/jhgkjhg_ugtdk77/article/details/45336235