标签：
3xN骨牌覆盖
在2xN的骨牌覆盖问题中，我们有递推式子 (0,1)xM^n=(f[n-1],f[n])。 我们考虑能否在3xN的情况下找到同样的式子。 但在实际的推导过程可以发现，对于3xN的覆盖，对应的f数值公式比2xN复杂太多。我们需要换个角度来思考推导公式。
在我们放置骨牌的过程中，一定是放好一行之后再放置下一行。根据摆放的方式，可能会产生很多种不同的形状，而这些形状之间是否具有某些递推关系呢？ 如果他们存在一定的递推关系，则我们可以根据第i行的方案数来推导第i+1行的方案数。这样一行一行推导，直到第N行时不就得到了我们要求的方案数了么？ 那么来研究一下是否存在这样的推导公式吧
假设我们已经放好了一些骨牌，对于当前最后一列(第i列)骨牌，可能有8种情况：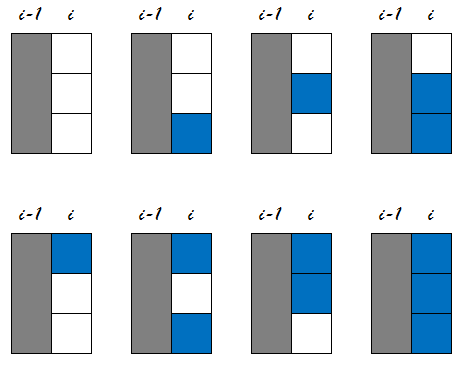 
对于上面这8种状态，我们用数字来标记它们。以有放置骨牌的格子为1，未放置为0，转化为2进制数 以最下面一行作为1，则有： 
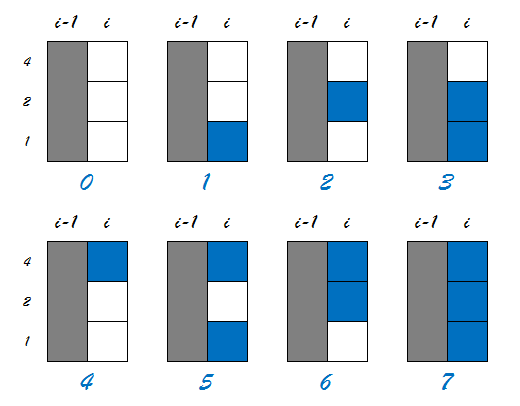接下来考虑如何放置骨牌，我们先将棋盘旋转一下。假设我们正在放置第i行的骨牌，那么会有下面3种方式： 
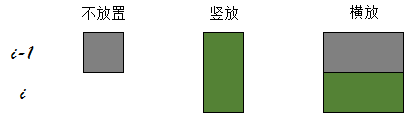灰色表示已经有的骨牌，绿色表示新放置的骨牌。 每一种放置方法解释如下，假设当第i行的状态为x，第i-1行的状态为y：
举个例子：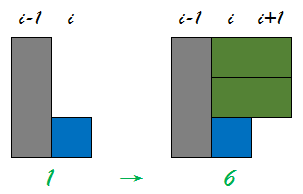 
对于第i行状态1，我们在第i+1行竖放两块骨牌之后便能到达状态6。 但是在这之中需要注意会出现下面这种情况： 
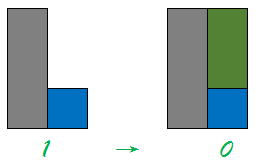这种情况看似是从状态1变成了状态0，其实是不对的。它不满足我们约定的放置方法，本质是第i行的状态1变成了第i行的状态7，而实际上我们应该放置的是第i+1行。 所以在枚举递推关系的时候一定要注意。 通过枚举8种状态到8种状态的转移，我们可以得到一个8x8的矩阵M（空白的地方均为0）： 
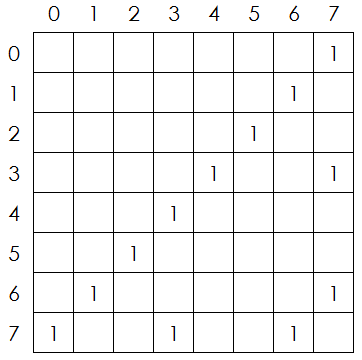m[i][j]表示从状态i变成状态j的方案数。
现在我们有了M矩阵，接下来考虑边界情况。 在2xN的骨牌覆盖中，有(0, 1)作为初始向量A，那么在3xN中初始向量A是如何呢？ 让我们先想想A向量所代表的含义。M矩阵表示状态到状态的转移，则A向量所表示的应该就是第0行各状态的方案数。 同理，对于A * M^n所求出的结果则应该表示为第n行各种状态的方案数。 那么A向量应该是多少呢？很显然，第0行在我们递推的过程中必须看作状态7才合理。故A向量表示为： {0, 0, 0, 0, 0, 0, 0, 1} 而对于我们寻求的答案，自然也是第n行放置为状态7的方案数了。
标签：
原文地址：http://www.cnblogs.com/yanglingwell/p/4464001.html
