标签:
本文内容基于《Accelerating exact k-means algorithms with geometric reasoning》
KDTree
k-means
k-means算法在初始化中心点后C通过以下迭代步骤得到局部最优解:
a.将数据集D中的点x赋给距离最近的中心点
b.在每个聚类中,重新计算中心点
传统算法中,a步需要计算n*k个距离(n为D的大小,k为聚类个数),b步需要相加n个数据点
而在KDTree中,每个非叶子节点,都存储了其包含的数据的数据范围信息h。
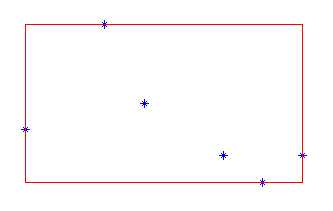 |
二维空间中的h可以使用矩形来表示 图中*为点,红色矩形为数据范围h |
a.
如果通过范围信息,能判断节点中数据都属于中心点c,则能省去节点中数据到中心点距离的计算
如果能判断h中数据都不属于某中心点c,则能省去节点中数据到中心点c距离的计算
b.
当知道节点中数据全部属于c,能将h中事先加好的统计量直接加到c的统计量中
KDTree的节点中存储的Max(各维度上的最大值)和Min(各维度上的最小值)确定了节点中数据的范围
中心点有(c1,c2,...,ck)
a.
判断是否可能存在
计算各中心点到h的最小距离(参考KDTree最近邻查找,第5步) d(ci,h)
如果存在一个最小距离,则这个ci可能是h的中心点(还需要进一步判断)
若存在不止一个最小距离,则h的中心点不存在,需要将h分割为更小(在h的左右树上)后查找
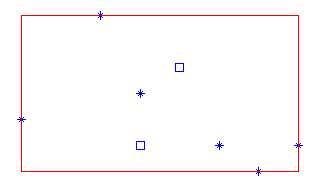 |
正方形表示的点都在h的内部 所以他们到h的最小距离相同,都为0 此h不存在中心点 |
b.
进一步判断,ci是否为中心点
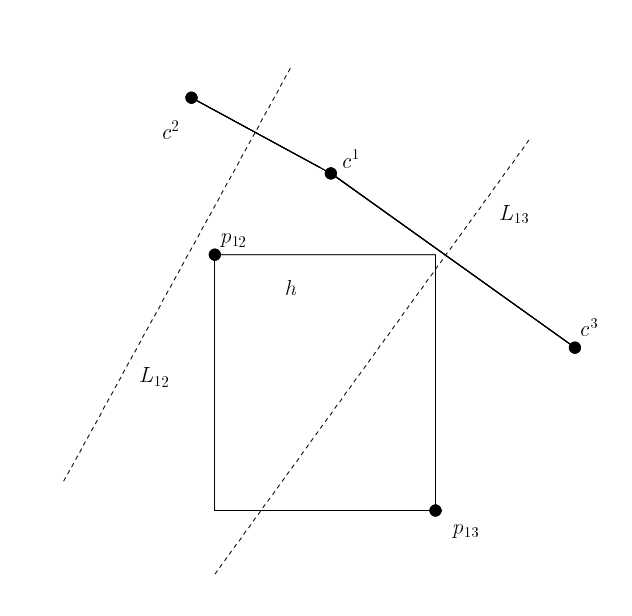 |
L12为c1和c2连线的中位线,h全部落在c1一边,
所以h中的全部点离c1比离c2近,称c1优于c2 而对于c1和c3来说,h有一部分落在c1,有一部分落在c3 c1不优于c3 |
|
判断c1是否优于c3:
取向量v=(c3-c1),找到点p属于h,使<v,p>内积最大 v各维度正负情况(+,-),则p在x轴上尽可能大,y轴上尽可能小,取到p13 p13离c3近,所以c1不优于c3 |
|
如果ci在优于其他点,则可以判定ci即为h的中心点;否则ci不是h的中心点;
虽然ci不是h的中心点,但是得到的信息,如ci优于c2,能将c2从h的子树的中心点候选列表中排除
|
KDTree中每个非叶子节点特殊属性: sumOfPoints:m维向量(m是数据的维度),其i维度的值为节点中数据第i维的和 n:节点中数据的个数 |
| 输入:KDTree,C 包括中心点(c1,c2,...,ck) |
| 输出:CNEW 新的k个中心点 |
| node=KDTree.root centers=k*m的数组//每行存储属于这个中心点的数据的和 datacount=k*1的数组//存储属于这个中心点的数据个数 |
|
UPDATE(node,C): IF node为叶子节点 遍历计算得到离node最近的节点ct centers[t]+=node.value; datacount[t]+=1; RETURN; FOR(ci in C) 计算d(ci,node.h) IF 有多个最小的d(ci,node.h) UPDATE(node.left,C); UPDATE(node.right,C); RETURN; //假设d(ci,node.h)最小的是ct CTOVER=[]//存储劣于ct的 FOR(ci in C(除了ct)) IF(ct 优于 ci) CTOVER.ADD(ci) IF(LEN(CTOVER)=LEN(C)-1)//ct优于其他的中心点 centers[t]+=node.sumOfPoints; datacount[t]+=node.n; RETURN; CT=(ci in C 且 ci not in CTOVER)//排除比ct差的中心点 UPDATE(node.left,CT); UPDATE(node.right,CT); RETURN; |
标签:
原文地址:http://www.cnblogs.com/porco/p/4466316.html