标签:
http://acm.hdu.edu.cn/showproblem.php?pid=3459
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 327670/327670 K (Java/Others)
Total Submission(s): 654 Accepted Submission(s): 234
Special Judge

分析:
题目不难理解,就是求还原的最小步数。
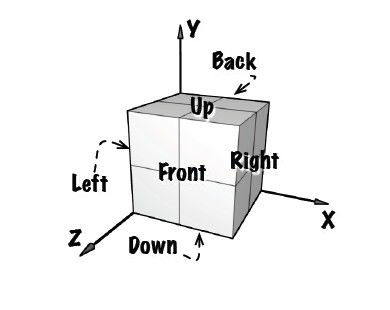
从图中不难看出,无论魔方怎么旋转,与原点相接的那个小方块是不动的,那么我们可以由原点的小方块得出三个面的最终颜色,然后再通过这三个面去确定其他三个面的颜色
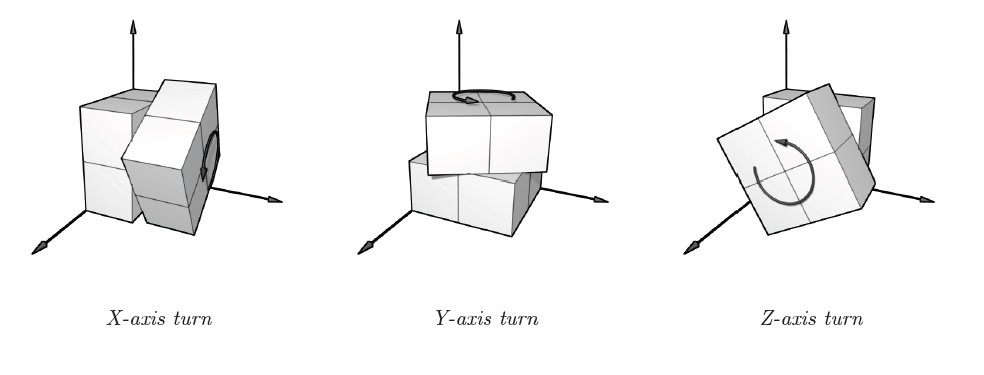
然后就是IDA的剪枝估测函数的h值,由于每次旋转能够改变8个小面,那么只要求出现在不在其位的面总数SUM,得出(sum+7)/8即可,加7是保证sum+7>=8得出步数。
AC代码:

1 #include <stdio.h> 2 #include <string.h> 3 #include <algorithm> 4 using namespace std; 5 6 struct node 7 { 8 int x,y; 9 } cube[10][10],side[10][10]; 10 11 char color[10],rubik[10][10]; 12 int ans[1000]; 13 int flag,step; 14 15 void init()//cube代表每个小立方体的3个面对应字符数字的哪个位置,side则是6个面,每个面的四个元素分别是什么 16 { 17 cube[0][0].x=3,cube[0][0].y=2; 18 cube[0][1].x=3,cube[0][1].y=1; 19 cube[0][2].x=4,cube[0][2].y=2; 20 cube[1][0].x=3,cube[1][0].y=3; 21 cube[1][1].x=3,cube[1][1].y=4; 22 cube[1][2].x=4,cube[1][2].y=3; 23 cube[2][0].x=2,cube[2][0].y=2; 24 cube[2][1].x=2,cube[2][1].y=1; 25 cube[2][2].x=1,cube[2][2].y=2; 26 cube[3][0].x=2,cube[3][0].y=3; 27 cube[3][1].x=1,cube[3][1].y=3; 28 cube[3][2].x=2,cube[3][2].y=4; 29 cube[4][0].x=3,cube[4][0].y=0; 30 cube[4][1].x=5,cube[4][1].y=2; 31 cube[4][2].x=3,cube[4][2].y=7; 32 cube[5][0].x=5,cube[5][0].y=3; 33 cube[5][1].x=3,cube[5][1].y=5; 34 cube[5][2].x=3,cube[5][2].y=6; 35 cube[6][0].x=0,cube[6][0].y=2; 36 cube[6][1].x=2,cube[6][1].y=7; 37 cube[6][2].x=2,cube[6][2].y=0; 38 cube[7][0].x=0,cube[7][0].y=3; 39 cube[7][1].x=2,cube[7][1].y=5; 40 cube[7][2].x=2,cube[7][2].y=6; 41 side[0][0].x=0,side[0][0].y=2; 42 side[0][1].x=0,side[0][1].y=3; 43 side[0][2].x=1,side[0][2].y=2; 44 side[0][3].x=1,side[0][3].y=3; 45 side[1][0].x=2,side[1][0].y=0; 46 side[1][1].x=2,side[1][1].y=1; 47 side[1][2].x=3,side[1][2].y=0; 48 side[1][3].x=3,side[1][3].y=1; 49 side[2][0].x=2,side[2][0].y=2; 50 side[2][1].x=2,side[2][1].y=3; 51 side[2][2].x=3,side[2][2].y=2; 52 side[2][3].x=3,side[2][3].y=3; 53 side[3][0].x=2,side[3][0].y=4; 54 side[3][1].x=2,side[3][1].y=5; 55 side[3][2].x=3,side[3][2].y=4; 56 side[3][3].x=3,side[3][3].y=5; 57 side[4][0].x=2,side[4][0].y=6; 58 side[4][1].x=2,side[4][1].y=7; 59 side[4][2].x=3,side[4][2].y=6; 60 side[4][3].x=3,side[4][3].y=7; 61 side[5][0].x=4,side[5][0].y=2; 62 side[5][1].x=4,side[5][1].y=3; 63 side[5][2].x=5,side[5][2].y=2; 64 side[5][3].x=5,side[5][3].y=3; 65 } 66 67 char get_color(int A,int B,int C) //通过小格子的颜色获得每个面的颜色 68 { 69 for(int i=0; i<8; i++) 70 { 71 if(rubik[cube[i][0].x][cube[i][0].y]==color[A]&&rubik[cube[i][1].x][cube[i][1].y]==color[B]&&rubik[cube[i][2].x][cube[i][2].y]!=color[C]) 72 return rubik[cube[i][2].x][cube[i][2].y]; 73 if(rubik[cube[i][1].x][cube[i][1].y]==color[A]&&rubik[cube[i][0].x][cube[i][0].y]==color[B]&&rubik[cube[i][2].x][cube[i][2].y]!=color[C]) 74 return rubik[cube[i][2].x][cube[i][2].y]; 75 if(rubik[cube[i][0].x][cube[i][0].y]==color[A]&&rubik[cube[i][2].x][cube[i][2].y]==color[B]&&rubik[cube[i][1].x][cube[i][1].y]!=color[C]) 76 return rubik[cube[i][1].x][cube[i][1].y]; 77 if(rubik[cube[i][2].x][cube[i][2].y]==color[A]&&rubik[cube[i][0].x][cube[i][0].y]==color[B]&&rubik[cube[i][1].x][cube[i][1].y]!=color[C]) 78 return rubik[cube[i][1].x][cube[i][1].y]; 79 if(rubik[cube[i][1].x][cube[i][1].y]==color[A]&&rubik[cube[i][2].x][cube[i][2].y]==color[B]&&rubik[cube[i][0].x][cube[i][0].y]!=color[C]) 80 return rubik[cube[i][0].x][cube[i][0].y]; 81 if(rubik[cube[i][2].x][cube[i][2].y]==color[A]&&rubik[cube[i][1].x][cube[i][1].y]==color[B]&&rubik[cube[i][0].x][cube[i][0].y]!=color[C]) 82 return rubik[cube[i][0].x][cube[i][0].y]; 83 } 84 } 85 86 void turn_x(char maze[10][10]) //x轴 87 { 88 char tmp; 89 tmp=maze[2][4]; 90 maze[2][4]=maze[2][5]; 91 maze[2][5]=maze[3][5]; 92 maze[3][5]=maze[3][4]; 93 maze[3][4]=tmp; 94 tmp=maze[1][3]; 95 maze[1][3]=maze[2][6]; 96 maze[2][6]=maze[5][3]; 97 maze[5][3]=maze[3][3]; 98 maze[3][3]=tmp; 99 tmp=maze[0][3]; 100 maze[0][3]=maze[3][6]; 101 maze[3][6]=maze[4][3]; 102 maze[4][3]=maze[2][3]; 103 maze[2][3]=tmp; 104 } 105 void turn_y(char maze[10][10]) //y轴 106 { 107 char tmp; 108 tmp=maze[2][0]; 109 maze[2][0]=maze[2][6]; 110 maze[2][6]=maze[2][4]; 111 maze[2][4]=maze[2][2]; 112 maze[2][2]=tmp; 113 tmp=maze[2][1]; 114 maze[2][1]=maze[2][7]; 115 maze[2][7]=maze[2][5]; 116 maze[2][5]=maze[2][3]; 117 maze[2][3]=tmp; 118 tmp=maze[0][2]; 119 maze[0][2]=maze[0][3]; 120 maze[0][3]=maze[1][3]; 121 maze[1][3]=maze[1][2]; 122 maze[1][2]=tmp; 123 } 124 void turn_z(char maze[10][10]) //z轴 125 { 126 char tmp; 127 tmp=maze[2][1]; 128 maze[2][1]=maze[1][3]; 129 maze[1][3]=maze[3][4]; 130 maze[3][4]=maze[4][2]; 131 maze[4][2]=tmp; 132 tmp=maze[3][1]; 133 maze[3][1]=maze[1][2]; 134 maze[1][2]=maze[2][4]; 135 maze[2][4]=maze[4][3]; 136 maze[4][3]=tmp; 137 tmp=maze[2][2]; 138 maze[2][2]=maze[2][3]; 139 maze[2][3]=maze[3][3]; 140 maze[3][3]=maze[3][2]; 141 maze[3][2]=tmp; 142 } 143 144 int get_h(char mid[10][10]) 145 { 146 int i,j,sum = 0; 147 for(i = 0; i<6; i++) 148 { 149 for(j = 0; j<4; j++) 150 { 151 if(mid[side[i][j].x][side[i][j].y]!=color[i]) 152 sum++; 153 } 154 } 155 return (sum+7)/8; 156 } 157 158 int IDA(char mid[10][10],int cnt) 159 { 160 if(cnt+get_h(mid)>step) 161 return 0; 162 if(cnt == step) 163 return 1; 164 for(int i = 0; i<3; i++) 165 { 166 char tem[10][10]; 167 for(int x = 0; x<6; x++) 168 for(int y = 0; y<8; y++) 169 tem[x][y]=mid[x][y]; 170 if(i == 0) 171 turn_x(tem); 172 else if(i == 1) 173 turn_y(tem); 174 else 175 turn_z(tem); 176 ans[cnt] = i; 177 if(IDA(tem,cnt+1)) 178 return 1; 179 } 180 return 0; 181 } 182 int main() 183 { 184 int i; 185 init(); 186 while(~scanf("%s",rubik[0])) 187 { 188 for(i = 1; i<6; i++) 189 scanf("%s",rubik[i]); 190 if(!strcmp(rubik[0],"........")) 191 break; 192 color[1]=rubik[3][0]; 193 color[5]=rubik[5][2]; 194 color[4]=rubik[3][7]; 195 color[0]=get_color(1,4,5); 196 color[2]=get_color(1,5,4); 197 color[3]=get_color(4,5,1); 198 step = 0; 199 while(1) 200 { 201 if(IDA(rubik,0)) break; 202 step++; 203 } 204 for(i = 0; i<step; i++) 205 printf("%c",ans[i]+‘X‘); 206 printf("\n"); 207 } 208 209 return 0; 210 }
标签:
原文地址:http://www.cnblogs.com/jeff-wgc/p/4467991.html