LCS(最长公共子序列)和dp(动态规划)

标签：

参照：v_JULY_v       

最长公共子序列定义：

        注意最长公共子串（Longest CommonSubstring）和最长公共子序列（LongestCommon Subsequence, LCS）的区别：子串（Substring）是串的一个连续的部分，子序列（Subsequence）则是从不改变序列的顺序，而从序列中去掉任意的元素而获得的新序列；更简略地说，前者（子串）的字符的位置必须连续，后者（子序列LCS）则不必。比如字符串acdfg同akdfc的最长公共子串为df，而他们的最长公共子序列是adf。LCS可以使用动态规划法解决。

LCS问题解决思路（dp算法）：

         1、事实上，最长公共子序列问题也有最优子结构性质。

    记:

Xi=﹤x1，?，xi﹥即X序列的前i个字符 (1≤i≤m)（前缀）

Yj=﹤y1，?，yj﹥即Y序列的前j个字符 (1≤j≤n)（前缀）

          假定Z=﹤z1，?，zk﹥∈LCS(X , Y)。

• 若xm=yn（最后一个字符相同），则不难用反证法证明：该字符必是X与Y的任一最长公共子序列Z（设长度为k）的最后一个字符，即有zk = xm = yn 且显然有Zk-1∈LCS(Xm-1 , Yn-1)即Z的前缀Zk-1是Xm-1与Yn-1的最长公共子序列。此时，问题化归成求Xm-1与Yn-1的LCS（LCS(X , Y)的长度等于LCS(Xm-1 , Yn-1)的长度加1）。

• 若xm≠yn，则亦不难用反证法证明：要么Z∈LCS(Xm-1, Y)，要么Z∈LCS(X , Yn-1)。由于zk≠xm与zk≠yn其中至少有一个必成立，若zk≠xm则有Z∈LCS(Xm-1 , Y)，类似的，若zk≠yn 则有Z∈LCS(X , Yn-1)。此时，问题化归成求Xm-1与Y的LCS及X与Yn-1的LCS。LCS(X , Y)的长度为：max{LCS(Xm-1 , Y)的长度, LCS(X , Yn-1)的长度}。

    由于上述当xm≠yn的情况中，求LCS(Xm-1 , Y)的长度与LCS(X , Yn-1)的长度，这两个问题不是相互独立的：两者都需要求LCS(Xm-1，Yn-1)的长度。另外两个序列的LCS中包含了两个序列的前缀的LCS，故问题具有最优子结构性质考虑用动态规划法。

    也就是说，解决这个LCS问题，你要求三个方面的东西：1、LCS（Xm-1，Yn-1）+1；2、LCS（Xm-1，Y），LCS（X，Yn-1）；3、max{LCS（Xm-1，Y），LCS（X，Yn-1）}。

   2、最长公共子序列的结构有如下表示：

    设序列X=<x₁, x₂, …, x_m>和Y=<y₁, y₂, …, y_n>的一个最长公共子序列Z=<z₁, z₂, …, z_k>，则：

1. 若x_m=y_n，则z_k=x_m=y_n且Z_k-1是X_m-1和Y_n-1的最长公共子序列；
2. 若x_m≠y_n且z_k≠x_{m ，}则Z是X_m-1和Y的最长公共子序列；
3. 若x_m≠y_n且z_k≠y_n ，则Z是X和Y_n-1的最长公共子序列。

    其中X_m-1=<x₁, x₂, …, x_m-1>，Y_n-1=<y₁, y₂, …, y_n-1>，Z_k-1=<z₁, z₂, …, z_k-1>。

   3、例如，设所给的两个序列为X=<A，B，C，B，D，A，B>和Y=<B，D，C，A，B，A>。如下图所示：

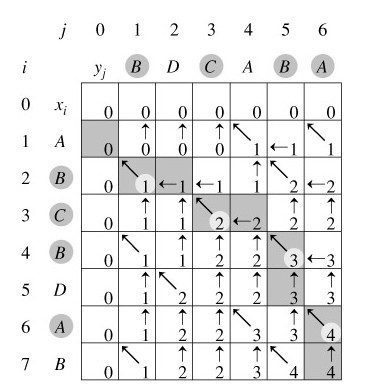
      看懂这个图，对lcs算法就理解的差不多了：

<span style="color: rgb(51, 51, 51);">                             </span><span style="color:#ff0000;">   if(str1.charAt(i-1)==str2.charAt(j-1)){
					dp[i][j]=dp[i-1][j-1]+1;
				}else{
					dp[i][j]=Math.max(dp[i-1][j], dp[i][j-1]);
				}</span>

代码实现：

public class LCS{  
    public static void main(String[] args){  
   
        //设置字符串长度  
        int substringLength1 = 20;  
        int substringLength2 = 20;  //具体大小可自行设置  
   
        // 随机生成字符串  
        String x = GetRandomStrings(substringLength1);  
        String y = GetRandomStrings(substringLength2);  
   
        Long startTime = System.nanoTime();  
        // 构造二维数组记录子问题x[i]和y[i]的LCS的长度  
        int[][] opt = new int[substringLength1 + 1][substringLength2 + 1];  
   
        // 动态规划计算所有子问题  
        for (int i = substringLength1 - 1; i >= 0; i--){  
            for (int j = substringLength2 - 1; j >= 0; j--){  
                if (x.charAt(i) == y.charAt(j))  
                    opt[i][j] = opt[i + 1][j + 1] + 1;                                 //参考上文我给的公式。  
                else  
                    opt[i][j] = Math.max(opt[i + 1][j], opt[i][j + 1]);        //参考上文我给的公式。  
            }  
        }  
        System.out.println(opt[20][20]);
}

LCS(最长公共子序列)和dp(动态规划)

标签：

原文地址：http://blog.csdn.net/u011479875/article/details/45393231