标签：
当我们写好一份源代码，提交给编译器的时候，这是编译器对我们提交代码进行词法分析。这个整个编译过程的第一步。词法分析器将我们的提交的代码看作是一个文本，它工作的目的就是将这个文本中不符合我们所使用的语言（c++或者java）的单词（字符串）挑选出来，以及将符合语言的单词（字符串）进行分类。
对于第一个功能，挑选不合格字符串，我们可以这样理解。例如，对于c++而言，定义变量名不能使用数字开头，那么如果出现 int 1tmp；语句就是非法的。
对于第二个功能，我们一方面要确定怎么解读一个字符串。例如，if32，是将其看成为if 和 32 ？还是将其看成if32？另一方面，我们要将其读到的字符串进行分类，例如，if 是内部关键字，它是属于IF类.但是对于int tmp； 中的tmp，它对于语言（c++或者其他语言）而言，就是一个id，因此它属于ID，而前面的int，则是INT.再比如对于43，它是一个常量，也是一个NUM，3.14则是一个REAL。
那么对于一段代码 int a = 10 , b = 20; int c ; c = a + b ; 经过词法处理后得到的输出为
INT ID ASSIGN NUM COMMA INT ID ASSIGN NUM SEMI(;) INT ID SEMI ID ASSIGN ID PLUS ID SEMI
上面的输出的符号，将用于语法分析时使用。很显然，语法分析只专注于分析一个单词是否合法，以及分类，并不处理单词与单词之间的关系是否合法。例如，
void func() { // action} ; int a = func ;
对于第二个语句，词法分析并不关心其是否正确，照样输出 INT ID ASSIGN ID SEMI.
了解了词法分析的作用后，乍一看，词法分析面对的处理对象似乎是一个单词，例如，先读入一个单词，判断这个单词的类型，再读入一个，判断类型，and so on。但是，如何判断是否读入了一个“正确”的单词呢？例如 , c=a+b 和 c = a + b 两个都是合法的c++语句。对于后者而言，可以用空格来表示读完一个单词，但是对于前者，词法分析器是将c=a+b看成一个单词呢？还是将c看成一个单词 ？
所以，词法分析器是将一个字母作为分析目标，根据该字母的下一个字母来判断是否应该判定该字母所属类型。对于c=a+b而言，当读入a时，词法分析其将其标记为ID状态，当读入＝号时，则表示a的状态已经可以确定，则将a的状态（ID）输出。再举个例子，tmp=c-d，当词法分析器读入t时，将其标记为ID状态，读入m和p时，状态不变，当读入＝时，输出当前状态，并退回到其实状态，然后对读入的＝进行分析。用画图来表示就是：
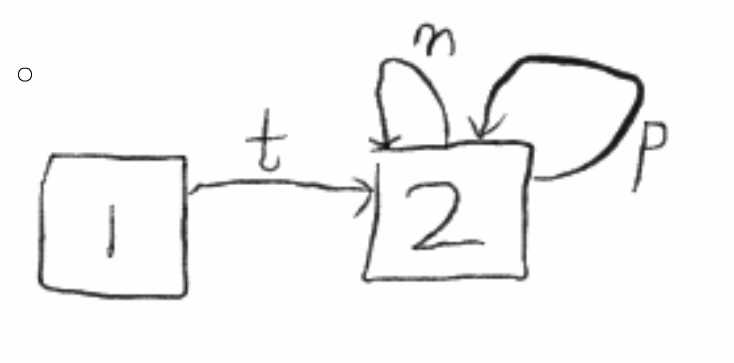（我保证这是我所有博客中唯一一张手绘图，务必珍惜。。。。。没见过健身完手抖的么）
方框2就是状态ID，状态1时开始状态，当读入t时，到达状态2.当读入m时转一圈回到2（上面标有m的带箭头的曲线，对的，曲线，不是头上的犄角），读入p时，也还回到状态2。当读入p时，发现没有地方可以走了，就输出状态2，也就是ID，然后回到状态1，如果状态1有一条标有＝的曲线指向另一个状态，那么就沿着那条曲线（我们成为边）到另一个状态。
我们把上图叫做一个状态机，因为它的状态时有限的，且只要读进一个字符我们就能确定找到唯一一条边，或者时找到一个状态，所以我们成为确定有限自动状态机（DFA）。
这样我们就知道每一个或者多个状态确定一个语言中的一个分类（初始状态除外），那么对于ID状态，c++中要求ID的不能用数字开头，那么就可以得到一下一个状态机，
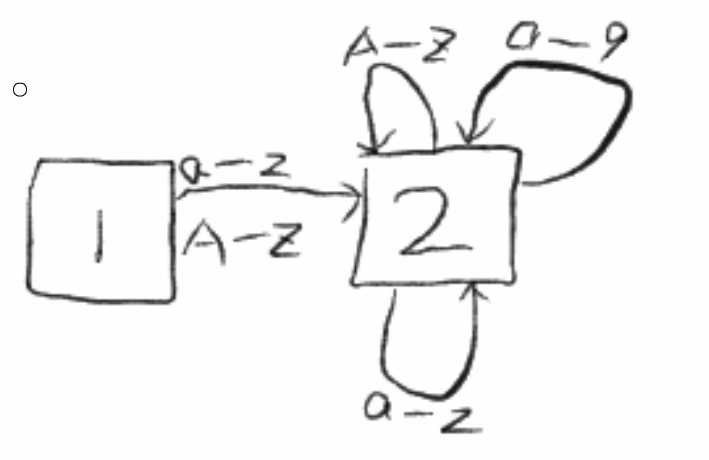（咳咳。。。。额，大家时来学知识的，不要在意保证不保证的这些细节，这不重要）
上图就描述了一个确定有限自动状态机，当在状态1的时候，读入任何以a-z和A-Z的字符都将进入状态2，在状态2中读入任何0-9，a－z，A－Z，都将回到状态2.如果读入一个其他的字符，状态机输出状态2（ID），然后回到状态1.（赶紧随便定义一个变量名试试吧）。
这样，只要将一个语言中的所有分类分别用一个DFA表示出来，再将各个DFA连接到一起，就可以对一个语言的源代码进行分析了。例如以下：
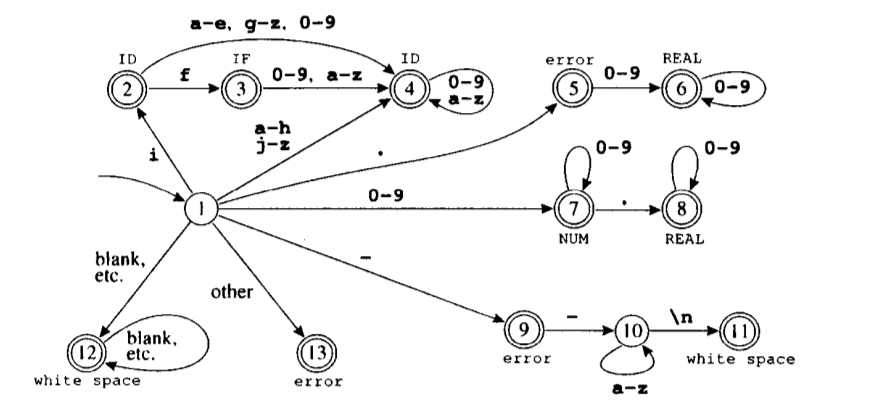
可以看出，这个大的状态机并不是简单的将几个小的状态机连接起来，还涉及到一些合并操作。
有以上可以看出来，确定一个语言的状态机，要解决两个问题，第一，如何描述语言中的一个类别，例如 REAL，IF，ID。第二，如果将各个小的状态机连接起来，组成一个大的语言确定有限状态机。
对于第一个问题，我们引入正则表达式（也称作正规式）。正则表达式的规定如下：
那么，如果要描述ID ，则其正则表达式为［a－zA－Z］＋[a-zA-Z0-9]* .正则表达式主要作用是使用flex词法分析器生成器。
对于第二问题，我们引入非确定有限状态机（NFA）。相比于确定有限自动状态机，非确定有限自动状态机中有一条或者多条边可以为空，或者有标有同一个符号的两条指向不同状态的边。例如下面两幅图：
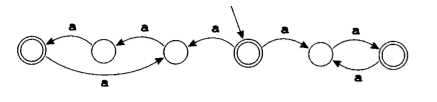
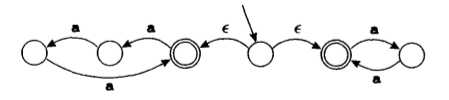
因为，当读入一个数据的时候，我们无法确定到底选择哪一条边，所以，是非确定的。
那么，将一个正则表达式转化成为一个确定有限状态机的过程为：正则表达式转化为非确定有限状态机，非确定有限状态机转化为确定有限状态机。
正则表达式转化为非确定有限状态机，可以使用下图：
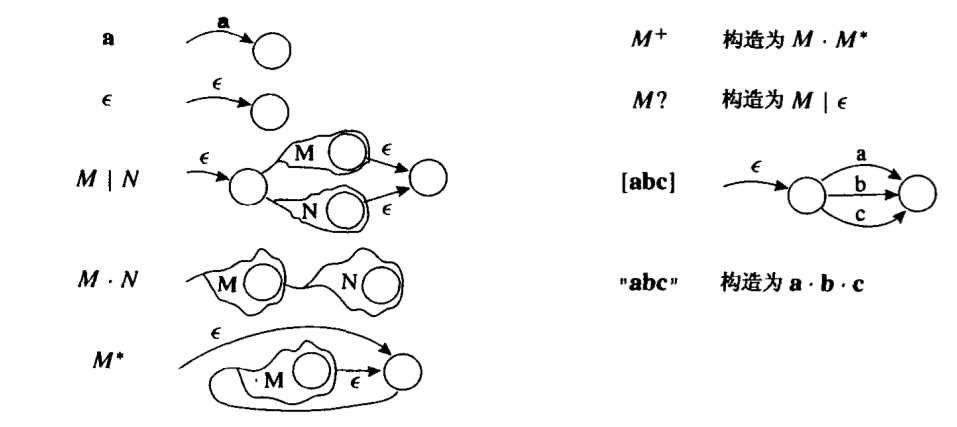
这样将语言中的所有类分别使用正则表达式表示出来，然后将每个正则表达式表示成一个小的非确定有限制状态机，然后使用一个新的状态作为起始状态，用空边将该起始状态和其他小的非确定有限状态机的起始状态连接起来，就得到该语言的非确定有限状态机。
为了将非确定有限状态机转化为确定有限状态机，我们引入ε闭包的概念：将状态集合A（包含一个或者多个状态）和使用空边和A连接的状态组成的新的状态集合，得到的新的状态集合成为closure（A），那么就有如下等式：
等式左边表示为：状态集合d吃掉一个标示符c后能够到达的状态的新状态集合（假设为）h。注意到因为有closure，所以h还包含使用空边和h中所有状态连接的状态。edge（s，c）标示从s出发，吃掉c后能到达的所有状态的集合。
我们根据以上等式，将下面的左图（NFA）转化为右图（DFA）：
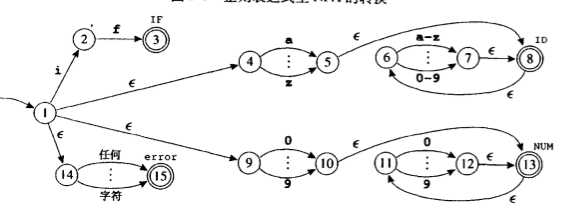
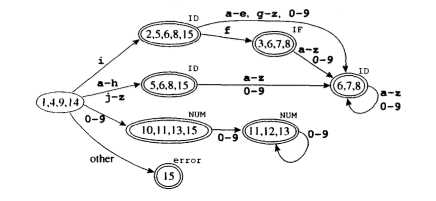
上图转化描述为：对于左图状态1，其ε闭包为A（1，4，9，14），就是右图中的开始状态集合。可以看出，这个集合A可以吃掉的字符包括i，a－z，0－9，以及任何字符（就是A中所有状态能够吃掉的字符的集合），如果A吃掉i（就是对A中的各个状态s求edge（s，i）），那么可以到达的集合为B`（2，5，15）,再求closure（B `）,则得到新的集合B（2，5，6，8，15）。然后考虑A吃掉（a－h，j－z），然后求闭包，那么得到集合C（5，6，8，15），等等。直到将A可以吃掉的字符都计算过后，我们就得到了上右图中，和起始状态集合连接的各个状态集合。然后依次再对其他状态集合进行相同操作。那么最终得到的式右图。这样就完成了NFA到DFA的转化。
如果将右图中的每个状态集合看成一个状态，那么就得到了一个确定有限自动状态机。那么，对于右图每个状态（或者状态集合），我们如何确定这个状态（状态集合）代表的是语言中的哪个类呢？也就是如何确定右图中的每个状态的上角标，如ID，NUM，IF等。这里有三个原则需要遵守：
第一：最长字符串原则。当我们遇到例如 if32i 这种字符串时，我们将对整个字符串进行匹配，而不是匹配到if就返回类型IF。
第二：终止状态优先原则。在我们从NFA转化到DFA过程中，如果一个状态集合包含终止状态，则在转化后得到的DFA中，该状态集合为终止状态集合。
第三：规则优先原则。如果转化后的状态集合包含多个终止状态，例如状态集合B中包含8和15，那么指定一个具有更高的规则优先级，在上面的例子中，我们指定8的规则优先级高，那么最终B代表的是ID类。那么在程序中如何指定呢？就是使用flex过程中，定义越靠前的正则表达式规则优先级越高。至于flex怎么使用，这不是我们的重点，可以参考其他资源。
好了，以上就是所有的词法分析过程，其实，最终我们是将一个DFA转化为一个二维数组，如下：
这是一个DFA数组的一部分。这个转化过程我们通常使用flex来完成。我们只要定义号一个语言的正则表达式，其他的NFA，DFA就直接交给flex来解决就可以了。但是，知道原理不是更让人自由么？
标签：
原文地址：http://www.cnblogs.com/BlackWalnut/p/4467749.html
