标签:
用SPSS的童鞋都知道,我们常用的方差分析(ANOVA)在一般线性模型(General Linear Model,简称GLM)的菜单下。那GLM是何许人也呢?让我们打开万能的wiki,键入General Linear Model。。。看到的居然是一张毫无违和感的Fitting Plot:

以及传说中的多元(线性)回归公式: $Y_{i}=\beta_{0} + \beta_{i1}X_{i1} + \beta_{2}X_{i2} + ... + \beta_{p}X_{ip} + \epsilon_{i} $
这不是回归问题么?跟检验差异的方差分析有何关系呢?
事实上,基于正态分布假设的参数检验(T检验,ANOVA,MANOVA,ANCOVA等等)均可以表征成回归问题。
不妨让我们以最简单的二类差异问题为例(组A与组B的差异) ,我们通常采用T检验考察A与B之间的差异,并用Error_bar来表示A与B的差异(如下图左)。
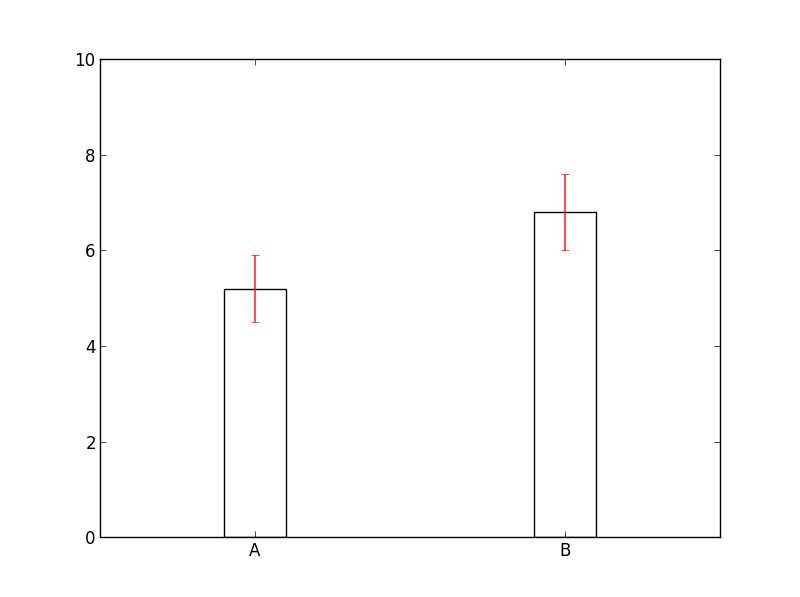
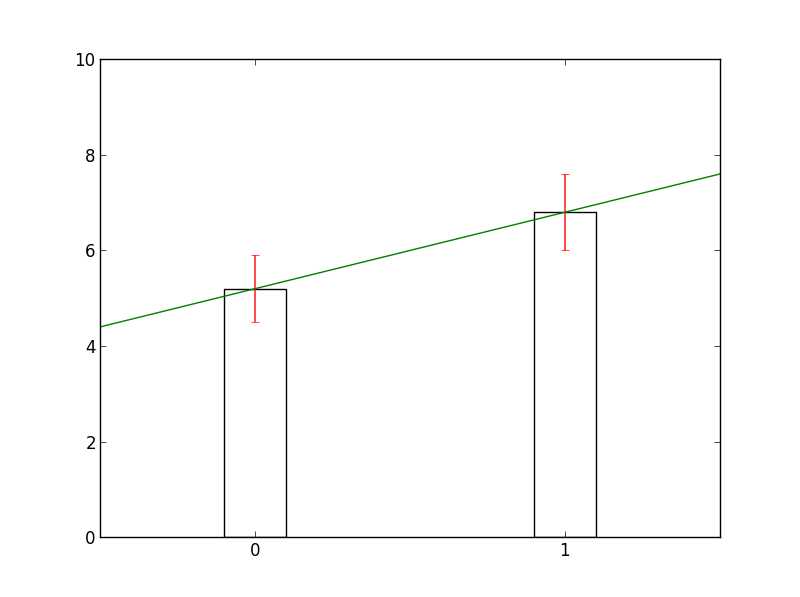
A与B是自变量X下的两个水平,我们可以用0(A)与1(B)来编码它们。那么,我们便可以得到因变量Y与自变量X的对应函数Y=F(X),假定两者之间存在线性相关,即有函数模型$Y = \alpha X + \beta$ (如上图右)。当A与B的差异越大,拟合线的斜率α也越大,即差异性检验可以通过回归的形式来表达。
那么两者之间的显著性是否等价呢?即A与B之间的T分数与拟合线的斜率α的T分数是否相同,答案是肯定的。
我们不妨假设组A与组B之间满足方差齐性,组A(Na)与组B(Nb)的样本数不等。那么组A与组B之间的t值即为
$$t=\frac{\overline{Y_{b}}-\overline{Y_{a}}}{S_{Y_{a}Y_{b}}· \sqrt{\frac{1}{N_{a}} + \frac{1}{N_{b}}}} $$
其中,有$S_{Y_{a}Y_{b}}=\sqrt{\frac{(N_{a}-1)S_{Y_{a}}^2 + (N_{b}-1)S_{Y_{b}}^2}{N_{a}+N_{b}-2}}$,$S_{Y_{a}}$、 $S_{Y_{b}}$ 分别为组A与组B的标准差。
令$MEAN=\overline{Y_{b}}-\overline{Y_{a}}$,$SE=S_{Y_{a}Y_{b}}·\sqrt{\frac{1}{N_{a}} + \frac{1}{N_{b}}}$ ,即有$t=\frac{MEAN}{SE}$
先处理最简单的MEAN部分:
将线性模型$Y = \alpha X + \beta$代入MEAN,由于$X_{a_{i}}=0$,$X_{b_{i}}=1$,即有: $MEAN =( \hat{\alpha} \times 1 +\hat{\beta} ) - ( \hat{\alpha} \times 0 +\hat{\beta} )={\hat{\alpha} -0} $
接着来看SE部分,首先是$S_{Y_{a}Y_{b}}$部分:
根据样本标准差的Bessel校正公式,$S_{Y_{a}}=\frac{ \sum_{i=1}^{N_{a}}{(Y_{a_{i}} - \overline{Y_{a}})^{2}}}{N_{a}-1}$,$S_{Y_{b}}=\frac{ \sum_{i=1}^{N_{b}}{(Y_{b_{i}} - \overline{Y_{b}})^{2}}}{N_{b}-1}$,将两者带入$S_{Y_{a}Y_{b}}$:
$$S_{Y_{a}Y_{b}}=\sqrt{\frac{\sum_{i=1}^{N_{a}}{(Y_{a_{i}} - \overline{Y_{a}})^{2}} + \sum_{i=1}^{N_{b}}{(Y_{b_{i}} - \overline{Y_{b}})^{2}}}{N_{a}+N_{b}-2}}$$
组A,B的均值分别是其组内点的最小二乘估计量,即$\overline{Y_{a}}=\hat{Y_{a_{i}}},i\in A$;$\overline{Y_{b}}=\hat{Y_{b_{i}}},i\in B$:
$$S_{Y_{a}Y_{b}}=\sqrt{\frac{\sum_{i=1}^{N_{a}}{(Y_{a_{i}} - \hat{Y_{a_{i}}})^{2}} + \sum_{i=1}^{N_{b}}{(Y_{b_{i}} - \hat{Y_{b_{i}}})^{2}}}{N_{a}+N_{b}-2}}=\sqrt{\frac{\sum_{i=1}^{N}{(Y_{i} - \hat{Y_{i}})^{2}}}{N-2}}$$
最后,来看$\sqrt{\frac{1}{N_{a}} + \frac{1}{N_{b}}}$:
$$\frac{1}{N_{a}} + \frac{1}{N_{b}}=\frac{1}{\frac{N_{a}N_{b}}{N_{a}+N_{b}}}$$
$$=\frac{1}{\frac{N_{b}(N-N_{b})}{N}}$$
$$=\frac{1}{N_{b} - \frac{N_{b}^2}{N}}$$
$$=\frac{1}{N_{b} - 2·\frac{N_{b}^2}{N}+\frac{N_{b}^2}{N}}$$
由于$X_{a_{i}}=0$,$X_{b_{i}}=1$,即有$N_{b}=\sum^{N}X_{i}=\sum^{N}X_{i}^2$,并有$\overline{X}=\frac{N_{b}}{N}$:
$$N_{b} - 2·\frac{N_{b}^2}{N}+\frac{N_{b}^2}{N}=\sum^{N}X_{i}^2-2·\sum^{N}(\frac{N_{b}}{N}·X_{i})+\sum^{N}(\frac{N_{b}}{N})^2$$
$$=\sum^{N}(X_{i}-\frac{N_{b}}{N})^2=\sum^{N}(X_{i}-\hat{X})^2$$
即$\large \sqrt{\frac{1}{N_{a}} + \frac{1}{N_{b}}}=\frac{1}{\sqrt{\sum_{i=1}^{N}(X_{i}-\overline{X})^2}}$
综上,$\Large t=\frac{MEAN}{SE}=\frac{MEAN}{S_{Y_{a}Y_{b}}·\sqrt{\frac{1}{N_{a}} + \frac{1}{N_{b}}}}=\frac{\hat{\alpha} -0}{\sqrt{\frac{\frac{1}{N-2}·\sum_{i=1}^{N}{(Y_{i} - \hat{Y_{i}})^{2}}}{\sum_{i=1}^{N}(X_{i}-\overline{X})^2}}}=\frac{\hat{\alpha} -0}{SE_{\hat{\alpha}}}$,最后的等式为线性模型的斜率的最小二乘估计量$\hat{\alpha}$是否大于0的T检验的表达式。
至此,我们成功的证明了:
方差齐性且不等组的组A与组B的之间的差异的T值 与
线性模型$Y = \alpha X + \beta$($X_{A}=0$,$X_{B}=1$)中$\alpha$是否显著大于0的T值是等价的。
对于更为一般的方差不齐的情况、配对样本T检验以及多组间比较的方差分析(dummy coding技术),且听下回分解^ ^
标签:
原文地址:http://www.cnblogs.com/lovedreamf/p/4462357.html