可并堆的实现

时间：2015-05-01 09:23:41 阅读：149 评论：0 收藏：0 [点我收藏+]

标签：

我要写三种可并堆,然后讲解它们.

1. 二项堆
2. 配对堆
3. RP堆

这三种堆都有一个共同特点,就是用一棵半满的树表示子堆,用一系列子堆表示整个堆(当然子堆是有限制的).那么我们可以很方便的进行合并两个堆等操作.

1.二项堆

这三种堆里最简单的就是二项堆了(Binomial Heap).为什么称为二项堆呢?二项堆这个小婊杂特别有趣,它的每个子堆大小都为2的幂.因此,它每次合并两个大小相等的堆,方法就像下面这张图.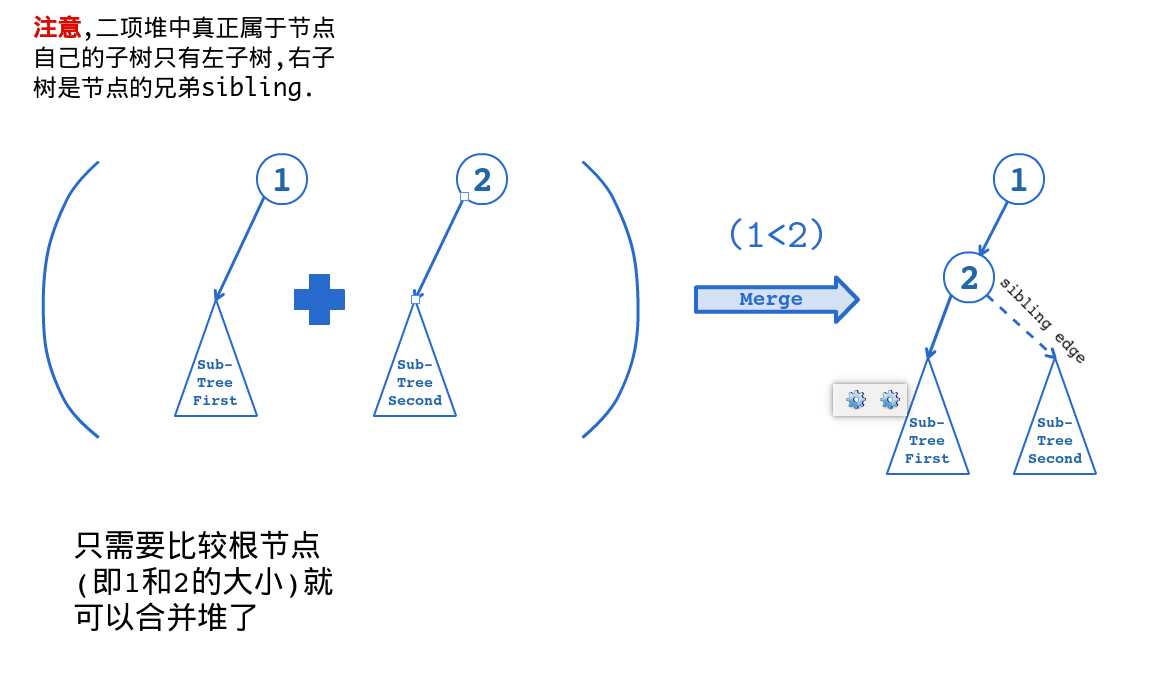 技术分享

那么手玩一下就可以得知,合并后两棵树其中的一棵向下偏了一位,层数多了一层.

那么深度为一时每层节点数是1(就一层)

深度为二时 1 1

3) 1 2 1
4) 1 3 3 1
5) 1 4 6 4 1

似曾相识?就是杨辉三角形.杨辉三角形的本质是什么?二项式.那么这个就被称为二项堆了.

二项堆的合并(merge)

二项堆的合并不难.我们只需要把所有深度相同的堆合并就可以了(还要用sibling指针串起来).

二项堆的插入(Insert)

新建一个二项堆,与原二项堆合并即可.

二项堆的最小值(Extract_min)

我们只需要边合并边维护即可.

二项堆的删除(Delete)

我们把以min为root的子堆提取出来,在原堆中删去,注意这是一棵只有左子节点的树.我们将左子结点这棵树当成二项堆,其中右子结点路径当成sibling指针(其实完全不用`当成‘),合并就行了.

二项堆实现

http://dsqiu.iteye.com/blog/1714961 这位大神实现了这三种堆(Bino,Fib,Pairing),但是我不建议看这个.

他的代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<climits>
using namespace std;
 
typedef struct BinHeapNode BinNode;
typedef struct BinHeapNode * BinHeap;
typedef struct BinHeapNode * Position;
 
//结点ADT
struct BinHeapNode {
    int key;
    int degree;
    Position parent;
    Position leftChild;
    Position sibling;
};
 
//用数组内的值建堆
BinHeap MakeBinHeapWithArray(int keys[], int n);
 
//两个堆合并
BinHeap BinHeapUnion(BinHeap &H1, BinHeap &H2);
 
//将H1, H2的根表合并成一个按度数的单调递增次序排列的链表
BinHeap BinHeapMerge(BinHeap &H1, BinHeap &H2);
 
//使H2成为H1的父节点
void BinLink(BinHeap &H1, BinHeap &H2);
 
//返回最小根节点的指针
BinHeap BinHeapMin(BinHeap heap);
 
//减少关键字的值
void BinHeapDecreaseKey(BinHeap heap, BinHeap x, int key);
 
//删除一个关键字
BinHeap BinHeapDelete(BinHeap &heap, int key);
 
//找出一个关键字
BinHeap BinHeapFind(BinHeap &heap, int key);
 
//打印输出堆结构
void PrintBinHeap(BinHeap heap);
 
//销毁堆
void DestroyBinHeap(BinHeap &heap);
 
//用数组内的值建堆
BinHeap MakeBinHeapWithArray(int keys[], int n) {
    BinHeap heap = NULL, newHeap = NULL;
    for (int i = 0; i < n; i++) {
        newHeap = (BinHeap) malloc(sizeof(BinNode));
        if (newHeap == NULL) {
            puts("Out of the Space");
            exit(1);
        }
        memset(newHeap, 0, sizeof(BinNode));
        newHeap->key = keys[i];
        if (NULL == heap) {
            heap = newHeap;
        } else {
            heap = BinHeapUnion(heap, newHeap);
            newHeap = NULL;
        }
    }
    return heap;
}
 
//两个堆合并
BinHeap BinHeapUnion(BinHeap &H1, BinHeap &H2) {
    Position heap = NULL, pre_x = NULL, x = NULL, next_x = NULL;
    heap = BinHeapMerge(H1, H2);
    if (heap == NULL) {
        return heap;
    }
 
    pre_x = NULL;
    x = heap;
    next_x = x->sibling;
 
    while (next_x != NULL) {
        if ((x->degree != next_x->degree) ||//Cases 1 and 2
            ((next_x->sibling != NULL) && (next_x->degree == next_x->sibling->degree))) {
                pre_x = x;
                x = next_x;
        } else if (x->key <= next_x->key) {//Cases 3
            x->sibling = next_x->sibling;
            BinLink(next_x, x);
        } else {//Cases 4
            if (pre_x == NULL) {
                heap = next_x;
            } else {
                pre_x->sibling = next_x;
            }
            BinLink(x, next_x);
            x = next_x;
        }
        next_x = x->sibling;
    }
    return heap;
}
 
//将H1, H2的根表合并成一个按度数的单调递增次序排列的链表
BinHeap BinHeapMerge(BinHeap &H1, BinHeap &H2) {
    //heap->堆的首地址，H3为指向新堆根结点
    BinHeap heap = NULL, firstHeap = NULL, secondHeap = NULL,
        pre_H3 = NULL, H3 = NULL;
 
    if (H1 != NULL && H2 != NULL){
        firstHeap = H1;
        secondHeap = H2;
        //整个while，firstHeap, secondHeap, pre_H3, H3都在往后顺移
        while (firstHeap != NULL && secondHeap != NULL) {
            if (firstHeap->degree <= secondHeap->degree) {
                H3 = firstHeap;
                firstHeap = firstHeap->sibling;
            } else {
                H3 = secondHeap;
                secondHeap = secondHeap->sibling;
            }
 
            if (pre_H3 == NULL) {
                pre_H3 = H3;
                heap = H3;
            } else {
                pre_H3->sibling = H3;
                pre_H3 = H3;
            }
            if (firstHeap != NULL) {
                H3->sibling = firstHeap;
            } else {
                H3->sibling = secondHeap;
            }
        }//while
    } else if (H1 != NULL) {
        heap = H1;
    } else {
        heap = H2;
    }
    H1 = H2 = NULL;
    return heap;
}
 
//使H2成为H1的父节点
void BinLink(BinHeap &H1, BinHeap &H2) {
    H1->parent = H2;
    H1->sibling = H2->leftChild;
    H2->leftChild = H1;
    H2->degree++;
}
 
//返回最小根节点的指针
BinHeap BinHeapMin(BinHeap heap) {
    Position y = NULL, x = heap;
    int min = INT_MAX;
 
    while (x != NULL) {
        if (x->key < min) {
            min = x->key;
            y = x;
        }
        x = x->sibling;
    }
    return y;
}
 
//抽取有最小关键字的结点
BinHeap BinHeapExtractMin(BinHeap &heap) {
    BinHeap pre_y = NULL, y = NULL, x = heap;
    int min = INT_MAX;
    while (x != NULL) {
        if (x->key < min) {
            min = x->key;
            pre_y = y;
            y = x;
        }
        x = x->sibling;
    }
 
    if (y == NULL) {
        return NULL;
    }
 
    if (pre_y == NULL) {
        heap = heap->sibling;
    } else {
        pre_y->sibling = y->sibling;
    }
 
    //将y的子结点指针reverse
    BinHeap H2 = NULL, p = NULL;
    x = y->leftChild;
    while (x != NULL) {
        p = x;
        x = x->sibling;
        p->sibling = H2;
        H2 = p;
        p->parent = NULL;
    }
 
    heap = BinHeapUnion(heap, H2);
    return y;
}
 
//减少关键字的值
void BinHeapDecreaseKey(BinHeap heap, BinHeap x, int key) {
    if(key > x->key) {
        puts("new key is greaer than current key");
        exit(1); //不为降键
    }
    x->key = key;
 
    BinHeap z = NULL, y = NULL;
    y = x;
    z = x->parent;
    while(z != NULL && z->key > y->key) {
        swap(z->key, y->key);
        y = z;
        z = y->parent;
    }
}
 
//删除一个关键字
BinHeap BinHeapDelete(BinHeap &heap, int key) {
    BinHeap x = NULL;
    x = BinHeapFind(heap, key);
    if (x != NULL) {
        BinHeapDecreaseKey(heap, x, INT_MIN);
        return BinHeapExtractMin(heap);
    }
    return x;
}
 
//找出一个关键字
BinHeap BinHeapFind(BinHeap &heap, int key) {
    Position p = NULL, x = NULL;
    p = heap;
    while (p != NULL) {
        if (p->key == key) {
            return p;
        } else {
            if((x =BinHeapFind(p->leftChild, key)) != NULL) {
                return x;
            }
            p = p->sibling;
        }
    }
    return NULL;
}
 
//打印输出堆结构
void PrintBinHeap(BinHeap heap) {
    if (NULL == heap) {
        return ;
    }
    Position p = heap;
 
    while (p != NULL) {
        printf(" (");
        printf("%d", p->key);
        //显示其孩子
        if(NULL != p->leftChild) {
            PrintBinHeap(p->leftChild);
        }
        printf(") ");
 
        p = p->sibling;
    }
}       
 
int kp1[8] = {12,
               7, 25,
              15, 28, 33, 41};
 
int kp2[20] = {18,
                3, 37,
                6, 8, 29, 10, 44, 30, 23, 2, 48, 31, 17, 45, 32, 24, 50, 55};
 
int kp4[23] = {37, 41,
               10, 28, 13, 77,
               1, 6, 16, 12, 25, 8, 14, 29, 26, 23, 18, 11, 17, 38, 42, 27};
int main() {
    BinHeap H1 = NULL;
    H1 = MakeBinHeapWithArray(kp1, 7);
    puts("第一个二叉堆H1:");
    PrintBinHeap(H1);
 
    BinHeap H2 = NULL;
    H2 = MakeBinHeapWithArray(kp2, 19);
    puts("\n\n第二个二叉堆H2:");
    PrintBinHeap(H2);
 
    BinHeap H3 = NULL;
    H3 = BinHeapUnion(H1, H2);
    puts("\n\n合并H1,H2后，得到H3:");
    PrintBinHeap(H3);
 
    BinHeap H4 = NULL;
    H4 = MakeBinHeapWithArray(kp4, 22);
    puts("\n\n用于测试提取和删除的二叉堆H4:");
    PrintBinHeap(H4);
 
    BinHeap extractNode = BinHeapExtractMin(H4);
    if (extractNode != NULL) {
        printf("\n\n抽取最小的值%d后：\n", extractNode->key);
        PrintBinHeap(H4);
    }
 
    extractNode = BinHeapExtractMin(H4);
    if (extractNode != NULL) {
        printf("\n\n抽取最小的值%d后：\n", extractNode->key);
        PrintBinHeap(H4);
    }
 
    extractNode = BinHeapExtractMin(H4);
    if (extractNode != NULL) {
        printf("\n\n抽取最小的值%d后：\n", extractNode->key);
        PrintBinHeap(H4);
    }
 
    BinHeapDelete(H4, 12);
    puts("\n\n删除12后：");
    PrintBinHeap(H4);
    return 0;
}

这份代码很长,而且其逻辑并不清晰.

我的代码

其实二项堆很好写的,只要你理解了,它需要考虑的细节甚至比二叉堆还少.

typedef struct heapNode hpn;
typedef struct heapNode* hpp;
typedef struct heapManager_simple hsimple;

struct heapNode{
	int value,rank;
	hpp child,sibling,parent;
};

inline hpp hnalloc(){
	return malloc(sizeof hpn);
}

struct heapManager_simple{
	hpp root,min,rank[22];
	inline hpp makeHeap(int n){
		root=min=hnalloc();
		memset(root,0,sizeof root);
		root->value=n;
		rank[0]=root;
	}
	inline hpp extract_min(){
		return min;
	}
	inline void assign(hpp rt){//this method requires a O(log n) search for the min root
		memset(rank,0,sizeof rank);
		root=min=rt;
		while(rt){
			rank[rt->rank]=rt;
			if(rt->value < min->value) min=y;
			rt=rt->sibling;
		}
	}
	inline hpp link(hpp a,hpp b){
		if(b->value < a->value) std::swap(a,b);
		++a->rank;
		b->parent=a;
		b->sibling=a->child;
		a->child=b;
		return a;
	}
	inline hpp merge(hpp A){
		hpp b=A;
		while(A){
			A=A->sibling;
			while(rank[b->rank]){
				b=link(rank[b->rank],b);
				if(!min || min->value > b->value) min=b;
				rank[b->rank]=NULL;
			}
		}
		return root;
	}
	inline void gen_sibling(){
		root=NULL;
		for(int i=21;~i;--i){
			if(rank[i]){
				rank[i]->sibling=root;
				root=rank[i];
			}
		}
	}
	hpp insert(int n){
		hpp b=hnalloc();
		memset(b,0,sizeof b);
		b->value=n;
		merge(b);
		gen_sibling();
		return b;
	}
	hpp delete_top(){
		rank[min->rank]=NULL;
		hpp a=min->child;
		free(min);
		min=NULL;
		merge(a);
		gen_sibling();
	}
};

我的代码用了一种特殊的维护方法.我们知道每个子堆的大小是2^rank,那么我们就可以直接用数组存不同rank的子堆,每次操作完再用gen_sibling统一生成sibling指针.用这个技巧可以省掉很多代码,而且可以简化逻辑,处理掉细节.

二项堆是严格log n的,可以可持久化,可以拿来搞K短路.时间复杂度$V\log{V}+E+K\log{k}$.

Decrease_key很好写,就和二叉堆差不多,就不写代码了.(其实是我忘记加了)

2.配对堆

配对堆是一种自适应的可并堆.

配对堆的思想基于对于一个堆来说,树越高则效率越好(假设有堆的限制).如果变成一条链,那就已经排好序了.

配对堆的合并方法与rank值无关.从这点上来说,配对堆就好像可并堆中的Splay.

配对堆可以与Dijkstra很好地配合,时间复杂度$O(E+V\log{V})$.

可并堆的实现

标签：

原文地址：http://www.cnblogs.com/tmzbot/p/4470349.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行