标签:数学
| Time Limit: 1000MS |
|
Memory Limit: 65536K |
| Total Submissions: 250 |
|
Accepted: 125 |
|
Special Judge |
Description
The con?guration of three circles packed inside a triangle such that each circle is tangent to the other two circles and to two of the edges of the triangle has been studied by many mathematicians for more than two centuries. Existence and uniqueness of such
circles for an arbitrary triangle are easy to prove. Many methods of numerical calculation or geometric construction of such circles from an arbitrarily given triangle have been discovered. Today, such circles are called the Malfatti circles.
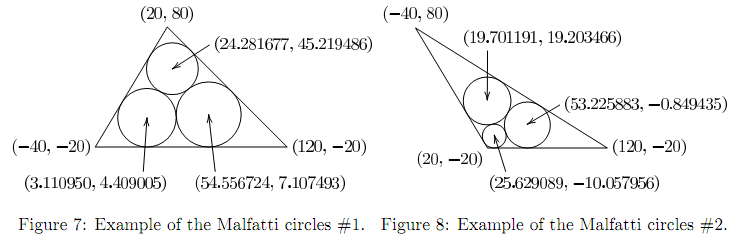
Figure 7 illustrates an example. The Malfatti circles of the triangle with the vertices (20, 80), (-40, -20) and (120, -20) are approximately
the circle with the center (24.281677, 45.219486) and the radius 21.565935,
the circle with the center (3.110950, 4.409005) and the radius 24.409005, and
the circle with the center (54.556724, 7.107493) and the radius 27.107493.
Figure 8 illustrates another example. The Malfatti circles of the triangle with the vertices (20, -20), (120, -20) and (-40, 80) are approximately
the circle with the center (25.629089, -10.057956) and the radius 9.942044,
the circle with the center (53.225883, -0.849435) and the radius 19.150565, and
the circle with the center (19.701191, 19.203466) and the radius 19.913790.
Your mission is to write a program to calculate the radii of the Malfatti circles of the given triangles.
Input
The input is a sequence of datasets. A dataset is a line containing six integers x1, y1, x2, y2, x3 and y3 in this order, separated by a space. The coordinates of the vertices of the given triangle are (x1, y1), (x2, y2) and (x3, y3), respectively. You can
assume that the vertices form a triangle counterclockwise. You can also assume that the following two conditions hold.
All of the coordinate values are greater than -1000 and less than 1000.
None of the Malfatti circles of the triangle has a radius less than 0.1.
The end of the input is indicated by a line containing six zeros separated by a space.
Output
For each input dataset, three decimal fractions r1, r2 and r3 should be printed in a line in this order separated by a space. The radii of the Malfatti circles nearest to the vertices with the coordinates (x1, y1), (x2, y2) and (x3, y3) should be r1, r2 and
r3, respectively.
None of the output values may have an error greater than 0.0001. No extra character should appear in the output.
Sample Input
20 80 -40 -20 120 -20
20 -20 120 -20 -40 80
0 0 1 0 0 1
0 0 999 1 -999 1
897 -916 847 -972 890 -925
999 999 -999 -998 -998 -999
-999 -999 999 -999 0 731
-999 -999 999 -464 -464 999
979 -436 -955 -337 157 -439
0 0 0 0 0 0
Sample Output
21.565935 24.409005 27.107493
9.942044 19.150565 19.913790
0.148847 0.207107 0.207107
0.125125 0.499750 0.499750
0.373458 0.383897 0.100456
0.706768 0.353509 0.353509
365.638023 365.638023 365.601038
378.524085 378.605339 378.605339
21.895803 22.052921 5.895714
题意:给出一个三角形的三个顶点的坐标,求三角形的三个内切圆,它们两两相切,并且每个顶点附近的圆和连接这个顶点的两条边也相切。求着三个内切圆的半径。
分析:套公式。
其中r为三角形内切圆的半径,s为半周长。
#include <cstdio>
#include <cmath>
using namespace std;
struct Point {
double x, y;
} A, B, C, I;
double get_dis(Point p1, Point p2) {
return sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
}
int main() {
while(~scanf("%lf%lf%lf%lf%lf%lf", &A.x, &A.y, &B.x, &B.y, &C.x, &C.y)) {
if(A.x == 0 && A.y == 0 && B.x == 0 && B.y == 0 && C.x == 0 && C.y == 0) break;
double a = get_dis(B, C);
double b = get_dis(A, C);
double c = get_dis(A, B);
double s = (a + b + c) / 2; // 半周长
I.x = (a * A.x + b * B.x + c * C.x) / (a + b + c);
I.y = (a * A.y + b * B.y + c * C.y) / (a + b + c); // 内切圆圆心坐标
double r = sqrt((s - a) * (s - b) * (s - c) / s); // 内切圆半径
double IA = get_dis(A, I);
double IB = get_dis(B, I);
double IC = get_dis(C, I);
double r1 = r / (2 * (s - a)) * (s - r + IA - IB - IC);
double r2 = r / (2 * (s - b)) * (s - r + IB - IA - IC);
double r3 = r / (2 * (s - c)) * (s - r + IC - IA - IB);
printf("%.6lf %.6lf %.6lf\n", r1, r2, r3);
}
return 0;
}
更多解释请见http://en.wikipedia.org/wiki/Malfatti_circles
POJ 3808 Malfatti Circles(计算几何)
标签:数学
原文地址:http://blog.csdn.net/lyhvoyage/article/details/45421663
