标签:
12. binary search Trees?
?
The search tree data structure supports many dynamic-set operations,including search ,minimum,maximum,predecessor,successor ,insert ,and delete.?
Thus, we can use a search tree both as a dictionary and as a priority queue.
因此,我们拿搜索树既可以用做字典,也可以用作优先队列。
12.1 what is a binary search tree ?
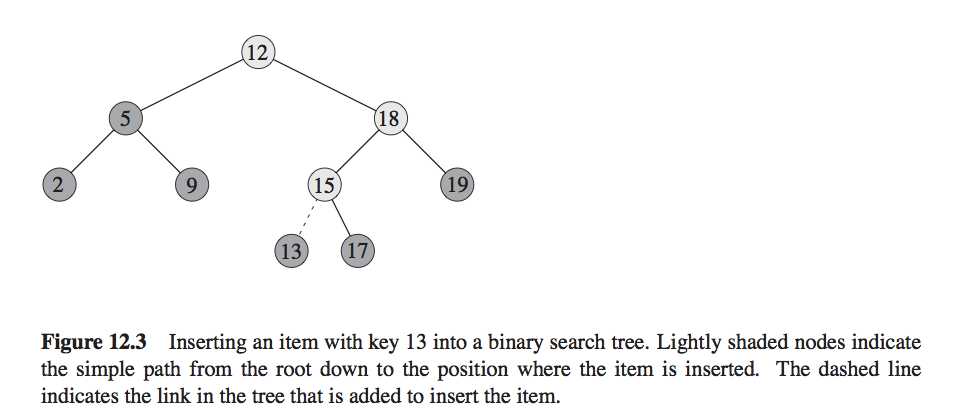
A binary search tree is organized, as the name suggests, in a binary tree, as shown in Figure 12.1.
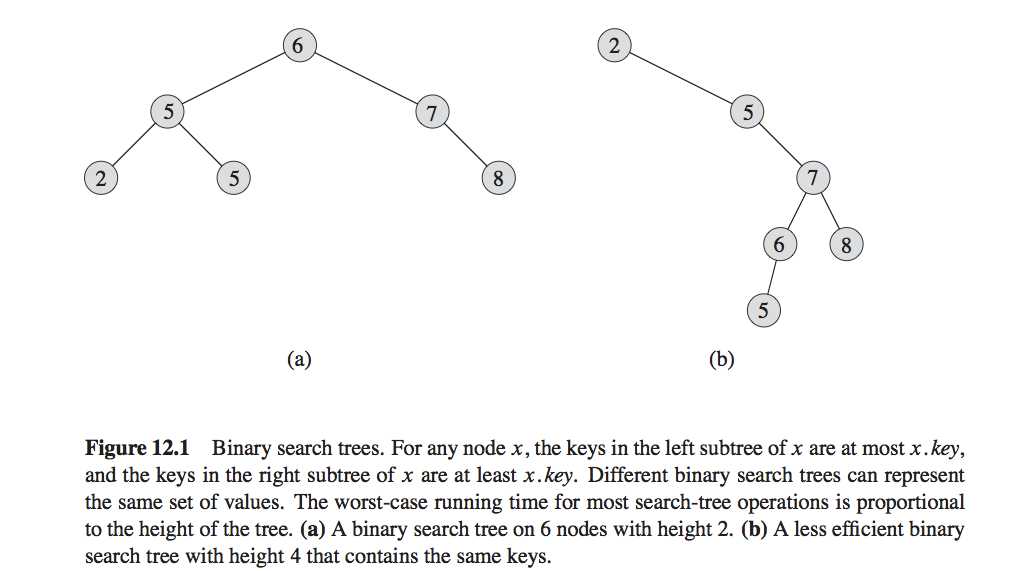
?
binary-search-tree property:
Let x be a node in a binary search tree. If y is a node in the left subtree of x, then y.key <=x:key. If y is a node in the right subtree of x, then y:key >= x:key.
二分搜索树的性质:
x是一个二分搜索树,如果y是x的左子树的一个节点,则y.key<=x.key ,如果y是x的右子树,则y.key>=x.key.
The binary-search-tree property allows us to print out all the keys in a binary search tree in sorted order by a simple recursive algorithm, called an inorder tree walk.
?
This algorithm is so named because it prints the key of the root of a subtree between printing the values in its left subtree and printing those in its right subtree.
?

?
12.2 Query a binary search tree.
Besides the SEARCH operation, binary search trees can support such queries as MINIMUM, MAXIMUM, SUCCESSOR, and PREDECESSOR
?
Searching?
Given a pointer to the root of the tree and a key k, TREE-SEARCH returns a pointer to a node with key k if one exists; otherwise, it returns NIL.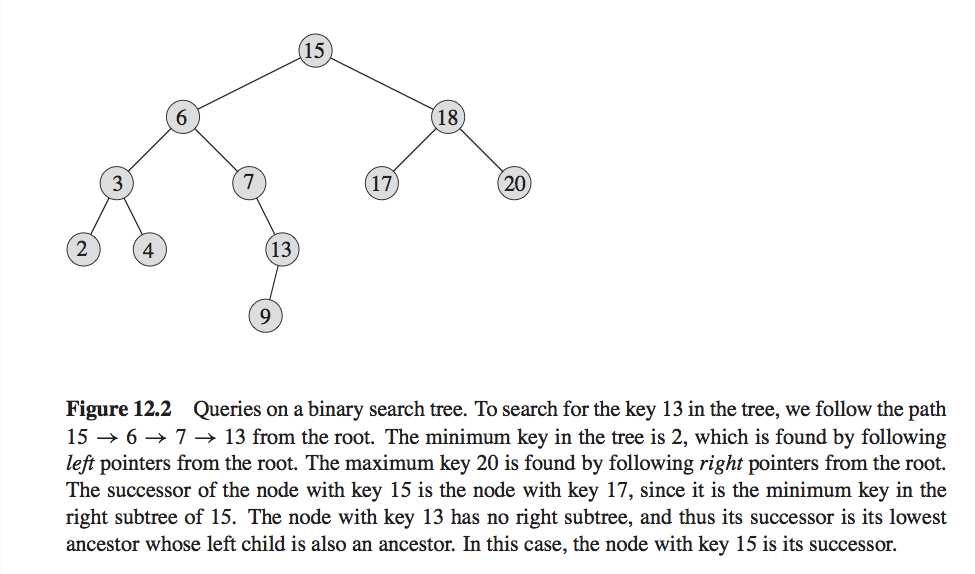


Minimum and maximum?
?
?
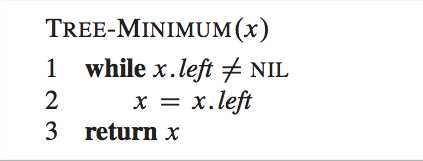
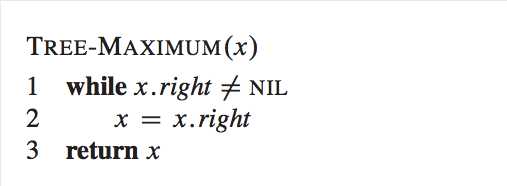
Successor and? predecessor?
Given a node in a binary search tree, sometimes we need to find its successor in the sorted order determined by an inorder tree walk.
给定一个节点,有时候我们需要找到利用in order tree wark?决定的顺序的继任者。
If all keys are distinct, the
successor of a node x is the node with the smallest key greater than x:key.
如果所有的关键字是不同的,那么节点x的接任者就是比x.key?大的最小值。
?

?
Insertion and deletion?
?
modifying the tree to insert a new element? is relatively straightforward,but handling deletion is somewhat more intricate .
?
插入相对直接,但是删除可能麻烦些。
?
INSERTION?
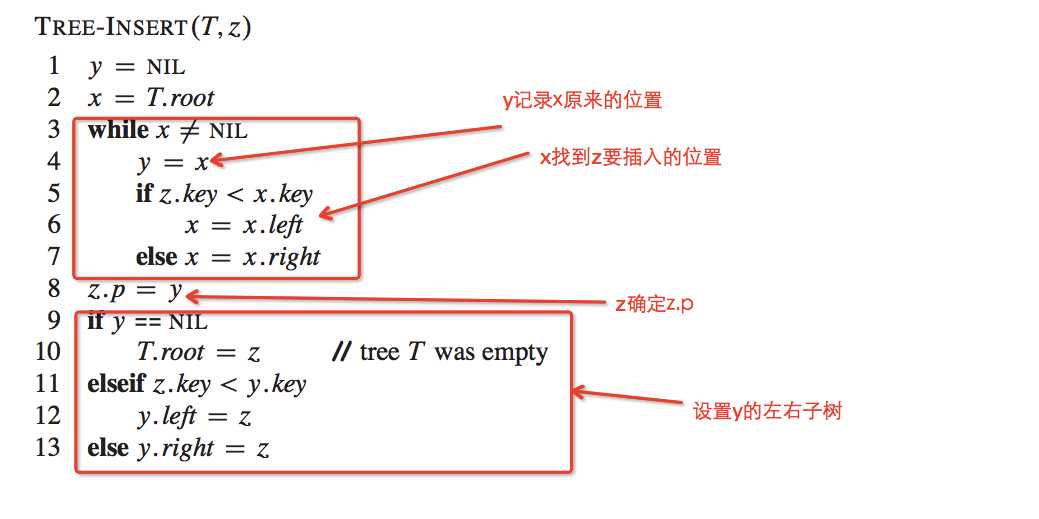
?
DELETION
?
The overall strategy for deleting a node ? from a binary search tree T has three basic cases but, as we shall see, one of the cases is a bit tricky.
?
If z has no children, then we simply remove it by modifying its parent to re- place ? with NIL as its child.
z没有孩子
If ? has just one child, then we elevate that child to take ?‘s position in the tree by modifying ?‘s parent to replace ? by ?‘s child.
?
If ? has two children, then we find ?‘s successor y—which must be in ?‘s right subtree—and have y take ?‘s position in the tree. The rest of ?‘s original right subtree becomes y‘s new right subtree, and ?‘s left subtree becomes y‘s new left subtree. This case is the tricky one because, as we shall see, it matters whether y is ?‘s right child.
?
?
It organizes its cases a bit differently from the three cases outlined previously by considering the four cases shown
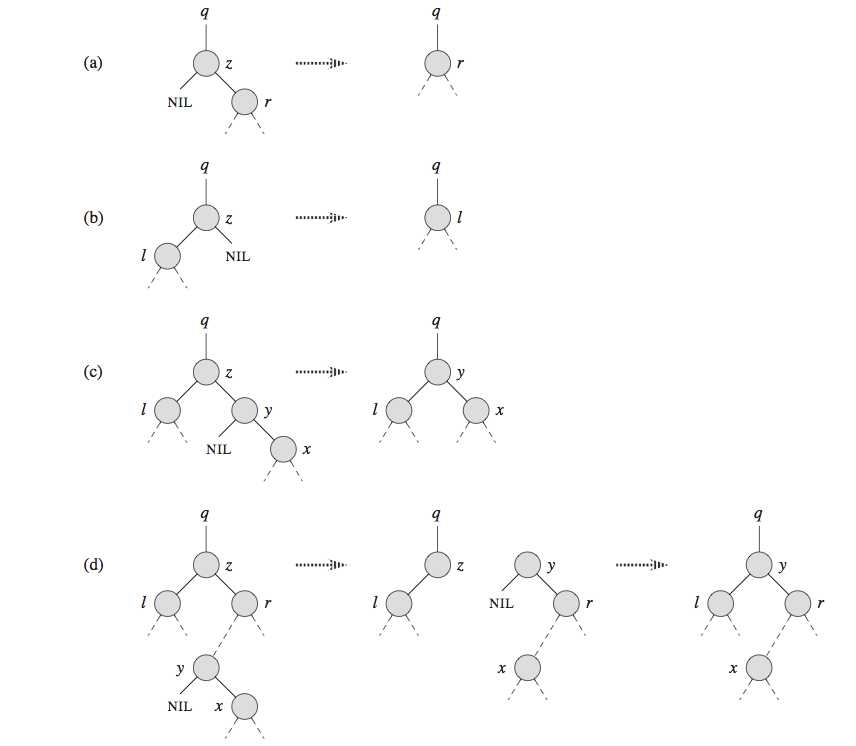
?
In order to move subtrees around within the binary search tree ,we define a subroutine Transplant ,which replaces one subtree as a child of its parent with another subtree.?
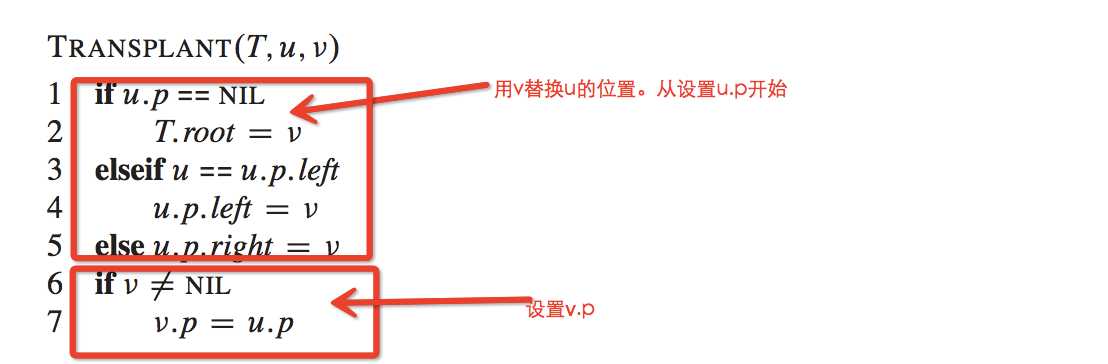
With the transplant procedure in hand ,here is the procedure that deletes node z from binary search tree T?:
?

?
标签:
原文地址:http://www.cnblogs.com/ljlkfx/p/4471385.html