标签:
欧拉函数:
φ(n)表示1~n中和n互素的数目
要处理出欧拉函数。先证明φ(p)=p-1.(p为素数)
根据互素的概念。两个数的公约数只有1,那么这两个数互素。再根据素数的定义。公约数除了本身以外只有1的数为素数。所以得证φ(p) = p-1.
再证明欧拉函数为不完全积性函数。
φ(m1*m2) = φ(m1)*φ(m2) 其中 m1和m2互素。即gcd(m1,m2)=1.
证明过程在我另外一篇博文中。我觉得那种证明比较好。当然还有别的比较好的证明方法。
http://www.cnblogs.com/Milkor/p/4464515.html
思考一个这样的经典问题。知道一个函数是积性的(其实只要是在两个互素数中的积性)。
那么根据算术基本定理(任何一个数可以拆分成素数的乘积形式)
φ(m) = φ(p1^k1) * φ(p2^k2) * φ(p3^k3) *...
那么我们只要求出φ(p^k)就可以求出任意数的对应的欧拉函数的对应值。
1~p^k 一共有p^k个数。
其中是p的倍数为 <p,2p,3p...p^k> (最后那个数可以列不等式找出来)。个数为p^k/p = p^(k-1).
所以和p^k互素的数的个数为 p^k - p^(k-1).
那么根据上述。可得
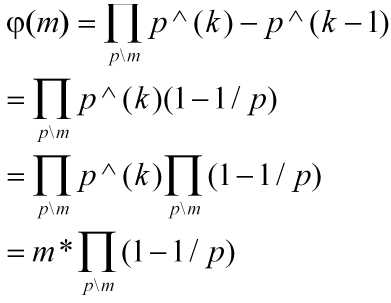
以上便是欧拉公式的来源。
顺便根据我们上述的推论,我们再推导一下线性筛法欧拉函数中。
当i%j==0的时候。也就是j为i的因子的时候。
φ(i*j)=φ(i)*j.这个结论吧。
证明过程:
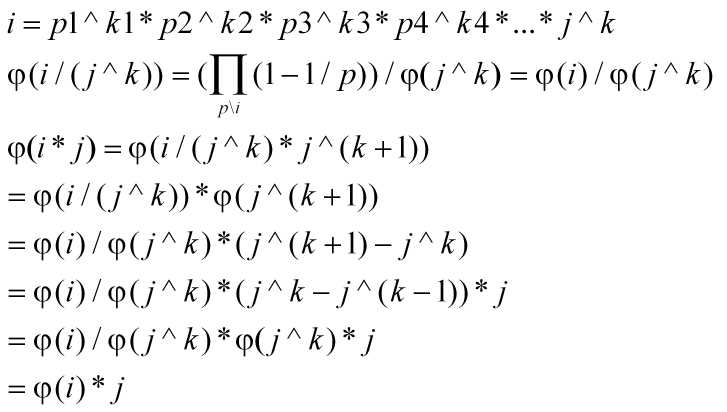

1 #include<stdio.h> 2 #include<string.h> 3 #define N 100 4 int prime[N+5]; 5 int num; 6 bool mark[N+5]; 7 int euler[N+5]; 8 void Euler() 9 { 10 int i,j; 11 num = 0; 12 memset(mark,0,sizeof(mark)); 13 euler[1] = 0; 14 for(i=2;i<=N;i++) 15 { 16 if(!mark[i]) 17 { 18 prime[num++] = i; 19 euler[i]=i-1; 20 } 21 for(j=0;j<num;j++) 22 { 23 if(i*prime[j]>N){break;} 24 mark[i*prime[j]] = 1; 25 if(i%prime[j]==0) 26 { 27 euler[i*prime[j]] = euler[i]*prime[j]; 28 } 29 else 30 { 31 euler[i*prime[j]] = euler[i]*euler[prime[j]]; 32 } 33 34 } 35 } 36 } 37 int main() 38 { 39 Euler(); 40 int i; 41 for(i=0;i<num;i++) 42 { 43 printf("%d ",prime[i]); 44 } 45 printf("\n"); 46 for(i=1;i<=N;i++) 47 { 48 printf("%d=%d ",i,euler[i]); 49 } 50 }
标签:
原文地址:http://www.cnblogs.com/Milkor/p/4471495.html