标签:
五一过完就是图论考试了,好吧,暂且放下糟糕的心情,继续投入到图论的复习工作中去,毕竟是图论考试,好好对待咯。
第一章:
概念与定理: 1.V(G)用来记录一个图的顶点集,E(G)用来记录一个图的边集。
2.根据图中边的有无方向,可以分为有向图和无向图。
3.简单图:既不含平行边又不含环的图称为简单图。特征:平行边,环
4.生成子图:G的生成子图是指满足V(H)=V(G)的子图。注意与子图的区别。
5.基础简单图:从图G中删去所有的环,并使每一对相邻顶点只留下一条边,即可得到G的一个简单生成子图,称为G的基础简单图。
6.用d(v)记录顶点v的度数。
7.显然:戴尔特G表示最大顶点度数,西塔G表示最小顶点度数
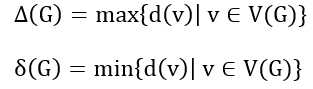
8.握手定理:总顶点度数等于总边数的两倍。推论:任何图中奇度数顶点的个数是偶数。(如果是奇数的话,就不符合总度数是偶数的握手定理了)
9.度序列:设G=(V,E)为一个v阶无向图,V={v1,v2,v3,v4...vu},称d(v1),d(v2),d(v3)...d(vu)为G的度序列。
10.度序列可图化:对于给定的非负整数序列d=(d1,d2,d3...dv),若存在以v={v1,v2,v3...vu}为顶点集的v阶无向图G,使得的d(vi)=di,则称d是可图化的。特别的,若所得的图是简单图,则称d是可简单图化的。
11.可图化定理:设非负整数列d=(d1,d2,d3...dv), 则d是可图化的,当且仅当总度数(即d1+d2+d3+...+dv)为0.
证明: 必要性:由握手定理易知显然成立
充分性:由已知条件可知,d中有2k(0<=k<=[v/2 +0.5])个奇数。不妨设它们d1,d2,d3...dk,dk+1...d2k.可用多种方法做出v阶无向图G=(V,E),V={v1,v2,v3...vu},比如边集如下产生:在顶点v r和v r+k之间连边,r=1,2...k.若di为偶数,令di‘=di,若di为奇数,令di‘=di-1,得d‘=(d‘1,d‘2,d‘3...d‘u),则d‘i均为偶数。再在vi处做出d‘i/2条环,i=1,2,3...u,将所得各条边集合组合在一起组成E,则G的度数为d。其实,di为偶数时,d(vi)=2*d‘i/2=2*di/2=di,di为奇数时,d(vi)=1+2*d‘i/2=1+d‘i=1+di-1=di.这就证明了d是可图化的。
标签:
原文地址:http://www.cnblogs.com/liugl7/p/4472713.html