标签:
题目链接:
http://acm.hdu.edu.cn/showproblem.php?pid=4565
题目大意:
给出a,b,n,m,求出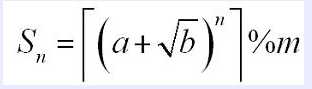 的值,
的值,
解题思路:
因为题目中出现了开根号,和向上取整后求余,所以用矩阵快速幂加速求解过程的时候,会产生误差,就很自然地想到了凑数,因为(a-1)^2<b<a^2,得出0<a-sqrt(b)<1,则无论n取多大,(a-sqrt(b))^n都是小于1的,(a-sqrt(b))^n 与 (a+sqrt(b))^n共轭,两者展开后会相互抵销,所以((a-sqrt(b))^n + (a+sqrt(b))^n)为整数,假设((a-sqrt(b))^n + (a+sqrt(b))^n)用sn表示,则sn*(a+sqrt(b))+(a-sqrt(b)) = Sn+1 - (a^2-b)*Sn-1,进一步得出 Sn+1 = 2*a*Sn - (a*a - b) * Sn-1,
代码:
1 #include <cstdio> 2 #include <cstring> 3 #include <cstdlib> 4 #include <algorithm> 5 #include <iostream> 6 #include <cmath> 7 #include <queue> 8 using namespace std; 9 #define LL __int64 10 LL a, b, n, m; 11 struct mat 12 { 13 LL p[2][2]; 14 }; 15 16 mat mul (mat x, mat y); 17 mat pow (mat x, mat y, LL z); 18 19 int main () 20 { 21 mat x, y; 22 while (scanf ("%I64d %I64d %I64d %I64d", &a, &b, &n, &m) != EOF) 23 { 24 memset (x.p, 0, sizeof(x.p)); 25 memset (y.p, 0, sizeof(y.p)); 26 x.p[0][0] = (2*(a*a+b)%m+m)%m;//要用long long,int相乘的时候会溢出 27 x.p[0][1] = (2*a) % m; 28 y.p[0][0] = (2*a) % m; 29 y.p[0][1] = 1; 30 y.p[1][0] = ((b-a*a)%m+m)%m; 31 //y.p[1][0] = ((b-a*a)+m)%m;//这样取余是错误的,因为还有可能是负数,害wa了好几次 32 x = pow (x, y, n-1); 33 printf ("%I64d\n", x.p[0][1]); 34 } 35 return 0; 36 } 37 38 mat mul (mat x, mat y) 39 { 40 int i, j, k; 41 mat z; 42 memset (z.p, 0, sizeof(z.p)); 43 for (i=0; i<2; i++) 44 for (j=0; j<2; j++) 45 { 46 for (k=0; k<2; k++) 47 z.p[i][j] += x.p[i][k] * y.p[k][j]; 48 z.p[i][j] = (z.p[i][j] + m )% m; 49 } 50 return z; 51 } 52 mat pow (mat x, mat y, LL z) 53 { 54 while (z) 55 { 56 if (z % 2) 57 x = mul(x,y); 58 y = mul (y, y); 59 z /= 2; 60 } 61 return x; 62 }
hdu 4565 So Easy! (共轭构造+矩阵快速幂)
标签:
原文地址:http://www.cnblogs.com/alihenaixiao/p/4473491.html