标签:
Let‘s play a puzzle using eight cubes placed on a 3 x 3 board leaving one empty square.
Faces of cubes are painted with three colors. As a puzzle step, you can roll one of the cubes to the adjacent
empty square. Your goal is to make the specified color pattern visible from above by a number of such steps.
The rules of this puzzle are as follows.
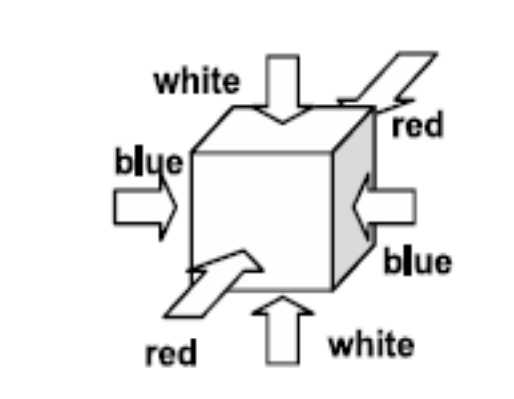
Coloring of Cubes: All the cubes are colored in the same way as shown in Figure 3. The opposite
faces have the same color.
Figure 3: Coloring of a cube
1.Initial Board State: Eight cubes are placed on the 3 x 3 board leaving one empty square. All the
cubes have the same orientation as shown in Figure 4. As shown in the figure, squares on the board
are given x and y coordinates, (1, 1), (1, 2), ..., and (3, 3). The position of the initially empty square
may vary.
Figure 4: Initial board state
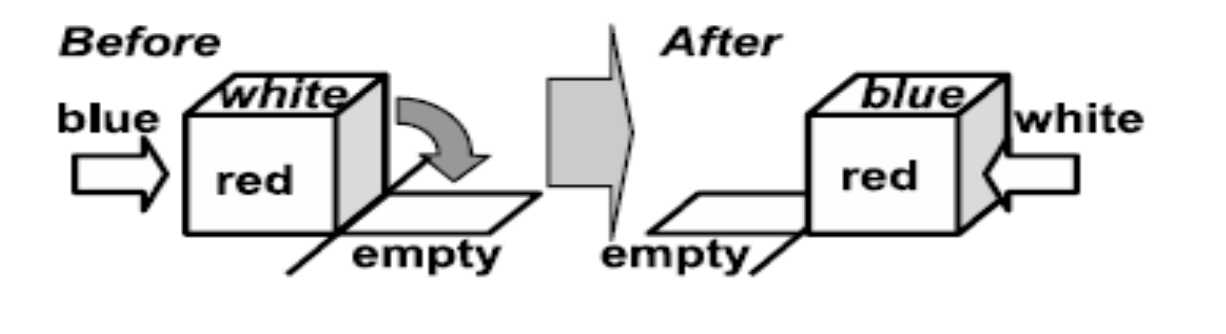
2.Rolling Cubes: At each step, we can choose one of the cubes adjacent to the empty square and roll it
into the empty square, leaving the original position empty. Figure 5 shows an example.
Figure 5: Rolling a cube
3.Goal: The goal of this puzzle is to arrange the cubes so that their top faces form the specified color
pattern by a number of cube rolling steps described above.
4.Your task is to write a program that finds the minimum number of steps required to make the specified color
pattern from the given initial state.
Input
The input is a sequence of datasets. The end of the input is indicated by a line containing two zeros separated
by a space. The number of datasets is less than 16. Each dataset is formatted as follows.
x y
F
11 F21 F31
F
12 F22 F32
F
13 F23 F33
The first line contains two integers x and y separated by a space, indicating the position (x, y) of the initially
empty square. The values of x and y are 1, 2, or 3.
The following three lines specify the color pattern to make. Each line contains three characters F1j, F2j, and
F
3j, separated by a space. Character Fij indicates the top color of the cube, if any, at position (i, j) as follows:
B:
Blue,
W:
White,
R:
Red,
E:
the square is Empty.
There is exactly one `E‘ character in each dataset.
Output
For each dataset, output the minimum number of steps to achieve the goal, when the goal can be reached
within 30 steps. Otherwise, output ``-1‘‘ for the dataset.
3618 - Cubic Eight-Puzzle 2/3
Sample Input
1 2
W W W
E W W
W W W
2 1
R B W
R W W
E W W
3 3
W B W
B R E
R B R
3 3
B W R
B W R
B E R
2 1
B B B
B R B
B R E
1 1
R R R
W W W
R R E
2 1
R R R
B W B
R R E
3 2
R R R
W E W
R R R
0 0
Sample Output
0
3
13
23
29
30
-1
-1
解题报告
难度。。很大,BFS这个没有疑问,那么究竟是A*还是双广呢,由于本题的状态数很多,且转移方程很麻烦,所以首先考虑A*.
估价函数这里不在多说(其实是我忘了),但提交后TLE...,CODE如下
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <queue> #include <ctime> using namespace std; const int MaxHashSize = 1526597; const int MaxState = 2500000; int tot,target[256]; char g[9]; int dir[4][2] = {0,1,0,-1,-1,0,1,0}; int getdia[6][4] = {5,5,2,2,3,3,4,4,4,4,0,0,1,1,5,5,2,2,1,1,0,0,3,3}; typedef struct status { char pos; char step; int g; char h; friend bool operator < (const status& a ,const status& b) { if (a.step + a.h < b.step + b.h) return false; if (a.step + a.h == b.step + b.h && a.step < b.step) return false; return true; } }; priority_queue<status> q; status start; int Head[MaxHashSize],Next[MaxState]; status st[MaxState]; void init_Hash() { memset(Head,-1,sizeof(Head)); } int GetHashValue(status &x) { return x.g % MaxHashSize; } bool insert_Hash(int id) { int h = GetHashValue(st[id]); int u = Head[h]; while(u != -1) { if (st[u].g == st[id].g) return false; u = Next[u]; } Next[id] = Head[h]; Head[h] = id; return true; } int caculateh(status &x) { int res = 0; int ok = 1; for(int i = 0 ; i < 9 ; ++ i) { int temp = 0; for(int j = 0 ; j < 3 ; ++ j) { int s = (x.g >> (3*i + j)) & 1; temp |= (s << j); } if ( (temp == 0 || temp == 1) && g[i] != ‘W‘) res ++ ; else if ( (temp == 2 || temp == 3) && g[i] !=‘R‘) res ++; else if ( (temp == 4 || temp == 5) && g[i] != ‘B‘) res ++; else if (temp == 7 && g[i] != ‘E‘ ) { res ++; ok = 0; } } if (ok) return res; else return res - 1; } int bfs() { int front = 0 ,rear = 1; q.push(start); while(!q.empty()) { status ss = q.top();q.pop(); st[front++] = ss; if (ss.h == 0) return ss.step; if (ss.h + ss.step > 30) return -1; int pos = ss.pos; int x = pos / 3; int y = pos % 3; int step = ss.step; int g = ss.g; for(int i = 0 ; i < 4 ; ++ i) { int newx = x + dir[i][0]; int newy = y + dir[i][1]; if (newx >= 3 || newx < 0 || newy >= 3 || newy < 0) continue; int newpos = newx * 3 + newy; status ns = ss; int temp = 0; for(int j = 0 ; j < 3 ; ++ j) { int s = (g >> (newpos * 3 + j) ) & 1; temp |= (s << j); } int sis = getdia[temp][i]; for(int j = 0 ; j < 3 ;++ j) ns.g |= (1 << (newpos*3 + j)); for(int j = 0 ; j < 3 ; ++ j) if (sis >> j & 1) ns.g |= (1 << pos * 3 + j); else ns.g &= ~(1 << pos * 3 + j); ns.step = step + 1; ns.pos = newpos; ns.h = caculateh(ns); st[rear] = ns; if (insert_Hash(rear)) { q.push(ns); rear++; } } } return -1; } int main(int argc, char * argv[]) { int kk = clock(); int s1,s2; while(scanf("%d%d%*c",&s1,&s2) && s1) { tot = 0; for(int i = 0 ; i < 9 ; ++ i) scanf("%c%*c",&g[i]); int fp = (s2-1) * 3 + s1 - 1; start.pos = fp; start.g = 0; init_Hash(); for(int i = 0 ; i < 3 ; ++ i) start.g |= (1 << (3*fp+i)); st[0] = start; insert_Hash(0); start.h = caculateh(start); start.step = 0; while(!q.empty()) q.pop(); cout << bfs() << endl; } cout << "Time use " << clock() - kk << endl; return 0; }
这里的代码中有Clock(),大家可以试试几组数据,30步的极限或者-1,速度非常慢。。(无法忍受)
那么,我们只能改用双广了,因为末状态有256种,所以我们用一个dfs把末状态压进去,提交后AC~
顺便多题一句双广复杂度是 2*n^(a/2) ,而单向的是n^a,code 如下
1 #include <iostream> 2 #include <algorithm> 3 #include <cstring> 4 #include <cstdio> 5 using namespace std; 6 const int MaxHashSize = 1526597; 7 const int MaxState = 2500000; 8 int tot,target[256],ssl; 9 char g[9]; 10 int dir[4][2] = {0,1,0,-1,-1,0,1,0}; 11 int getdia[6][4] = {5,5,2,2,3,3,4,4,4,4,0,0,1,1,5,5,2,2,1,1,0,0,3,3}; 12 13 14 typedef struct status 15 { 16 char pos; 17 char step; 18 int g; 19 }; 20 21 status start; 22 int Head[MaxHashSize],Next[MaxState]; 23 int Head2[MaxHashSize],Next2[MaxState]; 24 status st[MaxState]; 25 status st2[MaxState]; 26 27 void init_Hash() 28 { 29 memset(Head,-1,sizeof(Head)); 30 memset(Head2,-1,sizeof(Head)); 31 } 32 33 int GetHashValue(status &x) 34 { 35 return x.g % MaxHashSize; 36 } 37 38 bool insert_Hash(int id ,int l) 39 { 40 int h; 41 if (l == 0) 42 h = GetHashValue(st[id]); 43 else 44 h = GetHashValue(st2[id]); 45 int u; 46 if (l == 0) 47 u = Head[h]; 48 else 49 u = Head2[h]; 50 51 while(u != -1) 52 { 53 if (l == 0) 54 { 55 if (st[u].g == st[id].g) 56 return false; 57 u = Next[u]; 58 } 59 else 60 { 61 if (st2[u].g == st2[id].g) 62 return false; 63 u = Next2[u]; 64 } 65 } 66 if (l == 0) 67 { 68 Next[id] = Head[h]; 69 Head[h] = id; 70 } 71 else 72 { 73 Next2[id] = Head2[h]; 74 Head2[h] = id; 75 } 76 return true; 77 } 78 79 80 int meet(int id,int l) 81 { 82 int u,h; 83 if (l == 0) 84 { 85 h = GetHashValue(st[id]); 86 int u = Head2[h]; 87 while(u != -1) 88 { 89 if (st2[u].g == st[id].g) 90 return st[id].step + st2[u].step; 91 u = Next2[u]; 92 } 93 94 return -1; 95 } 96 else 97 { 98 h = GetHashValue(st2[id]); 99 int u = Head[h]; 100 while(u != -1) 101 { 102 if (st[u].g == st2[id].g) 103 return st[u].step + st2[id].step; 104 u = Next[u]; 105 } 106 107 return -1; 108 } 109 } 110 111 112 int bfs() 113 { 114 int front = 0 ,rear = 1; 115 int front2 = 0 , rear2 = 256; 116 while(front < rear && front2 < rear2) 117 { 118 if (1) 119 { 120 status ss = st[front++] ; 121 int ans = meet(front-1,0); 122 if (ans != -1) 123 return ans > 30 ? -1 : ans; 124 if (ss.step >= 30) 125 return -1; 126 int pos = ss.pos; 127 int x = pos / 3; 128 int y = pos % 3; 129 int step = ss.step; 130 int g = ss.g; 131 for(int i = 0 ; i < 4 ; ++ i) 132 { 133 int newx = x + dir[i][0]; 134 int newy = y + dir[i][1]; 135 if (newx >= 3 || newx < 0 || newy >= 3 || newy < 0) 136 continue; 137 int newpos = newx * 3 + newy; 138 status ns = ss; 139 int temp = 0; 140 for(int j = 0 ; j < 3 ; ++ j) 141 { 142 int s = (g >> (newpos * 3 + j) ) & 1; 143 temp |= (s << j); 144 } 145 int sis = getdia[temp][i]; 146 for(int j = 0 ; j < 3 ;++ j) 147 ns.g |= (1 << (newpos*3 + j)); 148 for(int j = 0 ; j < 3 ; ++ j) 149 if (sis >> j & 1) 150 ns.g |= (1 << pos * 3 + j); 151 else 152 ns.g &= ~(1 << pos * 3 + j); 153 ns.step = step + 1; 154 ns.pos = newpos; 155 st[rear] = ns; 156 if (insert_Hash(rear,0)) 157 { 158 rear++; 159 } 160 } 161 } 162 status ss = st2[front2++] ; 163 int ans = meet(front2-1,1); 164 if (ans != -1) 165 return ans > 30 ? -1 : ans; 166 if (ss.step >= 30) 167 return -1; 168 int pos = ss.pos; 169 int x = pos / 3; 170 int y = pos % 3; 171 int step = ss.step; 172 int g = ss.g; 173 for(int i = 0 ; i < 4 ; ++ i) 174 { 175 int newx = x + dir[i][0]; 176 int newy = y + dir[i][1]; 177 if (newx >= 3 || newx < 0 || newy >= 3 || newy < 0) 178 continue; 179 int newpos = newx * 3 + newy; 180 status ns = ss; 181 int temp = 0; 182 for(int j = 0 ; j < 3 ; ++ j) 183 { 184 int s = (g >> (newpos * 3 + j) ) & 1; 185 temp |= (s << j); 186 } 187 int sis = getdia[temp][i]; 188 for(int j = 0 ; j < 3 ;++ j) 189 ns.g |= (1 << (newpos*3 + j)); 190 for(int j = 0 ; j < 3 ; ++ j) 191 if (sis >> j & 1) 192 ns.g |= (1 << pos * 3 + j); 193 else 194 ns.g &= ~(1 << pos * 3 + j); 195 ns.step = step + 1; 196 ns.pos = newpos; 197 st2[rear2] = ns; 198 if (insert_Hash(rear2,1)) 199 { 200 rear2++; 201 } 202 } 203 } 204 return -1; 205 } 206 207 208 209 void dfs(int n,int temp) 210 { 211 if (n == 9) 212 { 213 st2[tot].g = temp; 214 st2[tot].step = 0; 215 insert_Hash(tot,1); 216 st2[tot++].pos = ssl; 217 } 218 else 219 { 220 int f; 221 if (g[n] == ‘W‘) 222 { 223 f = temp; 224 dfs(n+1,f); 225 f |= (1 << (3*n)); 226 dfs(n+1,f); 227 } 228 else if(g[n] == ‘R‘) 229 { 230 f = temp; 231 f |= (1 << (3*n+1)); 232 dfs(n+1,f); 233 f |= (1 << 3*n); 234 dfs(n+1,f); 235 } 236 else if(g[n] == ‘B‘) 237 { 238 f = temp; 239 f |= (1 << 3*n+2); 240 dfs(n+1,f); 241 f |= (1 << 3*n); 242 dfs(n+1,f); 243 } 244 else if(g[n] == ‘E‘) 245 { 246 f = temp; 247 for(int j = 0 ; j < 3 ; ++ j) 248 f |= (1 << 3*n + j); 249 dfs(n+1,f); 250 } 251 } 252 } 253 254 255 256 257 258 259 260 261 262 263 264 265 int main(int argc, char * argv[]) 266 { 267 int s1,s2; 268 while(scanf("%d%d%*c",&s1,&s2) && s1) 269 { 270 tot = 0; 271 for(int i = 0 ; i < 9 ; ++ i) 272 { 273 scanf("%c%*c",&g[i]); 274 if (g[i] == ‘E‘) 275 ssl = i; 276 } 277 int fp = (s2-1) * 3 + s1 - 1; 278 start.pos = fp; 279 start.g = 0; 280 init_Hash(); 281 dfs(0,0); 282 for(int i = 0 ; i < 3 ; ++ i) 283 start.g |= (1 << (3*fp+i)); 284 st[0] = start; 285 insert_Hash(0,0); 286 start.step = 0; 287 cout << bfs() << endl; 288 } 289 return 0; 290 }
UVA_Cubic Eight-Puzzle UVA 1604
标签:
原文地址:http://www.cnblogs.com/Xiper/p/4475845.html