标签:
uva11021 http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1962
给定n,k,m
有k个麻雀,每只活一天就会死,临死之前生出i只麻雀的概率为pi , 0<= i <n
问m天后,麻雀死光的概率
独立事件同时发生是每个事件的概率相乘, 每只麻雀都是独立的,只要求出一只麻雀m天后死亡的概率dp[m], 那么k只麻雀m天后死亡的概率为dp[m]^k
dp[i]表示i天后麻雀全部死亡的概率, 这个全部死亡即自己死亡,后代也死亡
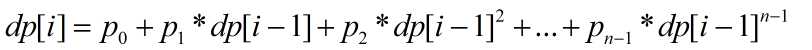
dp[i]可以分解为n个子事件,生0->n-1个孩子,如果生j个孩子,那么j个孩子要在i-1天后死亡,这样全部的麻雀才会在i天后死亡,j个孩子要在i-1天后死亡是独立事件同时发生
所以是dp[i-1]^j,生j个孩子的概率为pj, 所以生j个孩子且i-1天后死亡也是独立事件,概率为pj * dp[i-1]^j

1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef long long LL; 16 const int INF = 1<<30; 17 /* 18 f[i] = p0 19 */ 20 const int N = 1000 + 10; 21 double p[N],dp[N]; 22 int main() 23 { 24 int n, k, m, t, tCase = 1; 25 scanf("%d", &t); 26 while (tCase <= t) 27 { 28 scanf("%d%d%d", &n, &k, &m); 29 for (int i = 0; i < n; ++i) 30 scanf("%lf", &p[i]); 31 dp[0] = 0;//0天后死亡是不可能的,所以概率是0 32 dp[1] = p[0];//一天后死亡的概率是不生孩子的概率 33 for (int i = 2; i <= m; ++i) 34 { 35 dp[i] = 0; 36 for (int j = 0; j < n; ++j) 37 dp[i] += p[j] * pow(dp[i - 1], j); 38 } 39 printf("Case #%d: %.7lf\n", tCase++, pow(dp[m], k)); 40 } 41 return 0; 42 }
http://acm.hit.edu.cn/hoj/problem/view?id=2866
给定n,m 表示第一个人的血量和第二个人的血量
然后接下来两行,每行6个数字,分别表示摇骰子得到点数1->6的概率
要我们求第一个人赢的概率
p1,p2,p 表示进行一次游戏,第一个人赢,第二个人赢,平局的概率
q1,q2表示前n局中,第一个人赢一局,其他都是平局, 第二个人赢一局,其他都是平局的概率,如图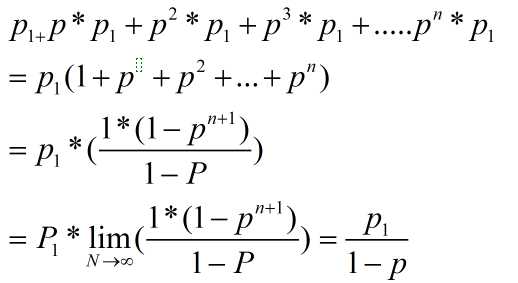
q1 = p1/(1-p)
q2 = p2/(1-p)
dp[i][j] 表示第一个人赢i次,第二个人赢j次, dp[i][j] = dp[i-1][j]*q1 + dp[i][j-1]*q2
为什么是dp[i][j] = dp[i-1][j]*q1 + dp[i][j-1]*q2;
而不是 dp[i][j] = dp[i-1][j]*p1 + dp[i][j-1]*p2;
因为进行一局游戏,有第一个人赢,第二个人赢,平局
不可能理想到只进行了一次游戏,就可能第一个人赢 即dp[i-1][j]*p1,
所以要一个人赢一局,可能经过了n局,然后才赢一局, q1,q2就是经过了很多平局,才赢得一局的情况
答案是dp[hp2][0->hp1-1]
初始化条件是dp[0][0] = 1,这是必然的,因为刚开始的,必定两个人都没有赢过一次,所以是1,必定发生

1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef long long LL; 16 const int INF = 1<<30; 17 /* 18 19 */ 20 double dp[2001][2001]; 21 int main() 22 { 23 int hp1, hp2; 24 double a[6], b[6]; 25 int i, j; 26 double p1, p2, p, q1, q2; 27 while (scanf("%d%d", &hp1, &hp2) != EOF) 28 { 29 p1 = p2 = p = q1 = q2 = 0; 30 for (i = 0; i < 6; ++i) 31 scanf("%lf", &a[i]); 32 for (i = 0; i < 6; ++i) 33 scanf("%lf", &b[i]); 34 for (i = 0; i < 6; ++i) 35 for (j = 0; j < i; ++j) 36 { 37 p1 += a[i] * b[j]; 38 p2 += a[j] * b[i]; 39 } 40 p = 1.0 - p1 - p2; 41 p == 1 ? q1 = q2 = 0 : q1 = p1 / (1 - p), q2 = p2 / (1 - p); 42 //q1 = p1 / (1.0 - p); 43 //q2 = p2 / (1.0 - p); 44 memset(dp, 0, sizeof(dp)); 45 dp[0][0] = 1.0; 46 for (i = 0; i <= hp2; ++i) 47 { 48 for (j = 0; j <= hp1; ++j) 49 { 50 if (j<hp1 && i) dp[i][j] += dp[i - 1][j] * q1; 51 if (i<hp2 && j) dp[i][j] += dp[i][j - 1] * q2; 52 } 53 } 54 double ans = 0; 55 for (j = 0; j < hp1; ++j) 56 ans += dp[hp2][j]; 57 printf("%.6lf\n", ans); 58 } 59 return 0; 60 }
标签:
原文地址:http://www.cnblogs.com/justPassBy/p/4476462.html