标签：

Random Walk

Yuanfang is walking on a chain. The chain has n nodes numbered from 1 to n. Every second, he can move from node i to node j with probability:



c(i,j) is an element in a given parameter matrix which is n×m. (1 <= c(i, j) <= 9)
Yuanfang wants to know the expectation time for him to walk from node 1 to node n.

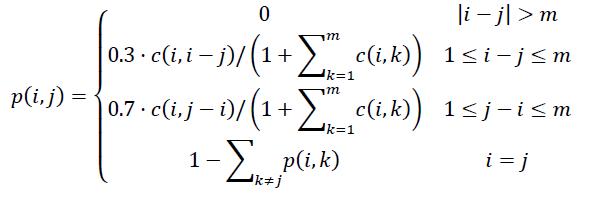
3 1
1
1
1
5 2
1 2
2 1
3 2
2 3
1 3
0 0

6.94
8.75

/* ***********************************************
Author        :CKboss
Created Time  :2015年05月06日 星期三 08时54分13秒
File Name     :HDOJ4579_2.cpp
************************************************ */

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <string>
#include <cmath>
#include <cstdlib>
#include <vector>
#include <queue>
#include <set>
#include <map>

using namespace std;

const int maxn=50050;
const double eps=1e-6;

double c[maxn][10];
double p[maxn][20];
double a[maxn][10];
double b[maxn];
double dp[maxn];

int n,m;

int main()
{
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);

	while(scanf("%d%d",&n,&m)!=EOF)
	{
		if(n==0&&m==0) break;
		for(int i=1;i<=n;i++)
		{
			double s=0;
			for(int j=1;j<=m;j++)
			{
				scanf("%lf",&c[i][j]);
				s+=c[i][j];
			}
			c[i][0]=s;
		}
		for(int i=1;i<=n;i++)
		{
			/// Left
			double sum=0.;
			for(int j=1;j<=m;j++)
			{
				if(i-j<1) continue;
				p[i][m-j]=0.3*c[i][j]/(1+c[i][0]);
				sum+=p[i][m-j];
			}
			/// Right
			for(int j=1;j<=m;j++)
			{
				if(i+j>n) continue;
				p[i][m+j]=0.7*c[i][j]/(1+c[i][0]);
				sum+=p[i][m+j];
			}
			p[i][m]=-sum;
			b[i]=-1;
		}

		for(int i=1;i<=m+1&&i<=n;i++) a[1][i]=p[1][m+i-1];
		
		for(int i=2;i<n;i++)
		{
			int start=max(1,i-m);
			int end=min(n,i+m);

			for(int j=start;j<i;j++) // 第j行去减第i行
			{
				if(fabs(p[i][m-i+j])<eps) continue;
				double t=p[i][m-i+j]/a[j][1];
				for(int k=1;k<=m+1&&j+k-1<=n;k++)
				{
					p[i][m-i+j+k-1]-=a[j][k]*t;
				}
				b[i]-=t*b[j];
			}

			for(int j=1;j<=end-i+1;j++)
			{
				a[i][j]=p[i][m+j-1];
			}
		}

		dp[n]=0;
		for(int i=n-1;i>=1;i--)
		{
			for(int j=2;j<=m+1&&i+j-1<=n;j++)
				b[i]-=dp[i+j-1]*a[i][j];
			dp[i]=b[i]/a[i][1];
		}

		printf("%.2f\n",dp[1]);
	}
    
    return 0;
}

HDOJ 4579 Random Walk 解方程

标签：

原文地址：http://blog.csdn.net/ck_boss/article/details/45532975