标签:
在前面的文章中,介绍了三种常见的分类算法。分类作为一种监督学习方法,要求必须事先明确知道各个类别的信息,并且断言所有待分类项都有一个类别与之对应。但是很多时候上述条件得不到满足,尤其是在处理海量数据的时候,如果通过预处理使得数据满足分类算法的要求,则代价非常大,这时候可以考虑使用聚类算法。聚类属于无监督学习,相比于分类,聚类不依赖预定义的类和类标号的训练实例。本文首先介绍聚类的基础——距离与相异度,然后介绍一种常见的聚类算法——k均值和k中心点聚类,最后会举一个实例:应用聚类方法试图解决一个在体育界大家颇具争议的问题——中国男足近几年在亚洲到底处于几流水平。
在正式讨论聚类前,我们要先弄清楚一个问题:如何定量计算两个可比较元素间的相异度。用通俗的话说,相异度就是两个东西差别有多大,例如人类与章鱼的相异度明显大于人类与黑猩猩的相异度,这是能我们直观感受到的。但是,计算机没有这种直观感受能力,我们必须对相异度在数学上进行定量定义。
设,其中X,Y是两个元素项,各自具有n个可度量特征属性,那么X和Y的相异度定义为:
,其中R为实数域。也就是说相异度是两个元素对实数域的一个映射,所映射的实数定量表示两个元素的相异度。
下面介绍不同类型变量相异度计算方法。
标量也就是无方向意义的数字,也叫标度变量。现在先考虑元素的所有特征属性都是标量的情况。例如,计算X={2,1,102}和Y={1,3,2}的相异度。一种很自然的想法是用两者的欧几里得距离来作为相异度,欧几里得距离的定义如下:
其意义就是两个元素在欧氏空间中的集合距离,因为其直观易懂且可解释性强,被广泛用于标识两个标量元素的相异度。将上面两个示例数据代入公式,可得两者的欧氏距离为:
除欧氏距离外,常用作度量标量相异度的还有曼哈顿距离和闵可夫斯基距离,两者定义如下:
曼哈顿距离:
闵可夫斯基距离:
欧氏距离和曼哈顿距离可以看做是闵可夫斯基距离在p=2和p=1下的特例。另外这三种距离都可以加权,这个很容易理解,不再赘述。
下面要说一下标量的规格化问题。上面这样计算相异度的方式有一点问题,就是取值范围大的属性对距离的影响高于取值范围小的属性。例如上述例子中第三个属性的取值跨度远大于前两个,这样不利于真实反映真实的相异度,为了解决这个问题,一般要对属性值进行规格化。所谓规格化就是将各个属性值按比例映射到相同的取值区间,这样是为了平衡各个属性对距离的影响。通常将各个属性均映射到[0,1]区间,映射公式为:
其中max(ai)和min(ai)表示所有元素项中第i个属性的最大值和最小值。例如,将示例中的元素规格化到[0,1]区间后,就变成了X’={1,0,1},Y’={0,1,0},重新计算欧氏距离约为1.732。
所谓二元变量是只能取0和1两种值变量,有点类似布尔值,通常用来标识是或不是这种二值属性。对于二元变量,上一节提到的距离不能很好标识其相异度,我们需要一种更适合的标识。一种常用的方法是用元素相同序位同值属性的比例来标识其相异度。
设有X={1,0,0,0,1,0,1,1},Y={0,0,0,1,1,1,1,1},可以看到,两个元素第2、3、5、7和8个属性取值相同,而第1、4和6个取值不同,那么相异度可以标识为3/8=0.375。一般的,对于二元变量,相异度可用“取值不同的同位属性数/单个元素的属性位数”标识。
上面所说的相异度应该叫做对称二元相异度。现实中还有一种情况,就是我们只关心两者都取1的情况,而认为两者都取0的属性并不意味着两者更相似。例如在根据病情对病人聚类时,如果两个人都患有肺癌,我们认为两个人增强了相似度,但如果两个人都没患肺癌,并不觉得这加强了两人的相似性,在这种情况下,改用“取值不同的同位属性数/(单个元素的属性位数-同取0的位数)”来标识相异度,这叫做非对称二元相异度。如果用1减去非对称二元相异度,则得到非对称二元相似度,也叫Jaccard系数,是一个非常重要的概念。
分类变量是二元变量的推广,类似于程序中的枚举变量,但各个值没有数字或序数意义,如颜色、民族等等,对于分类变量,用“取值不同的同位属性数/单个元素的全部属性数”来标识其相异度。
序数变量是具有序数意义的分类变量,通常可以按照一定顺序意义排列,如冠军、亚军和季军。对于序数变量,一般为每个值分配一个数,叫做这个值的秩,然后以秩代替原值当做标量属性计算相异度。
对于向量,由于它不仅有大小而且有方向,所以闵可夫斯基距离不是度量其相异度的好办法,一种流行的做法是用两个向量的余弦度量,其度量公式为:
其中||X||表示X的欧几里得范数。要注意,余弦度量度量的不是两者的相异度,而是相似度!
在讨论完了相异度计算的问题,就可以正式定义聚类问题了。
所谓聚类问题,就是给定一个元素集合D,其中每个元素具有n个可观察属性,使用某种算法将D划分成k个子集,要求每个子集内部的元素之间相异度尽可能低,而不同子集的元素相异度尽可能高。其中每个子集叫做一个簇。
与分类不同,分类是示例式学习,要求分类前明确各个类别,并断言每个元素映射到一个类别,而聚类是观察式学习,在聚类前可以不知道类别甚至不给定类别数量,是无监督学习的一种。目前聚类广泛应用于统计学、生物学、数据库技术和市场营销等领域,相应的算法也非常的多。本文仅介绍一种最简单的聚类算法——k均值(k-means)算法。
k均值算法的计算过程非常直观:
1、从D中随机取k个元素,作为k个簇的各自的中心。
2、分别计算剩下的元素到k个簇中心的相异度,将这些元素分别划归到相异度最低的簇。
3、根据聚类结果,重新计算k个簇各自的中心,计算方法是取簇中所有元素各自维度的算术平均数。
4、将D中全部元素按照新的中心重新聚类。
5、重复第4步,直到聚类结果不再变化。
6、将结果输出。
由于算法比较直观,没有什么可以过多讲解的。下面,我们来看看k-means算法一个有趣的应用示例:中国男足近几年到底在亚洲处于几流水平?
今年中国男足可算是杯具到家了,几乎到了过街老鼠人人喊打的地步。对于目前中国男足在亚洲的地位,各方也是各执一词,有人说中国男足亚洲二流,有人说三流,还有人说根本不入流,更有人说其实不比日韩差多少,是亚洲一流。既然争论不能解决问题,我们就让数据告诉我们结果吧。
下图是我采集的亚洲15只球队在2005年-2010年间大型杯赛的战绩(由于澳大利亚是后来加入亚足联的,所以这里没有收录)。
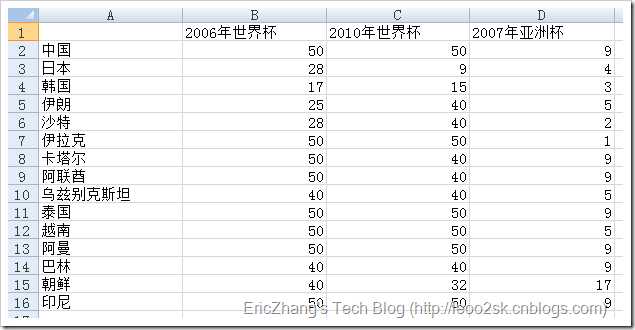
其中包括两次世界杯和一次亚洲杯。我提前对数据做了如下预处理:对于世界杯,进入决赛圈则取其最终排名,没有进入决赛圈的,打入预选赛十强赛赋予40,预选赛小组未出线的赋予50。对于亚洲杯,前四名取其排名,八强赋予5,十六强赋予9,预选赛没出现的赋予17。这样做是为了使得所有数据变为标量,便于后续聚类。
下面先对数据进行[0,1]规格化,下面是规格化后的数据:
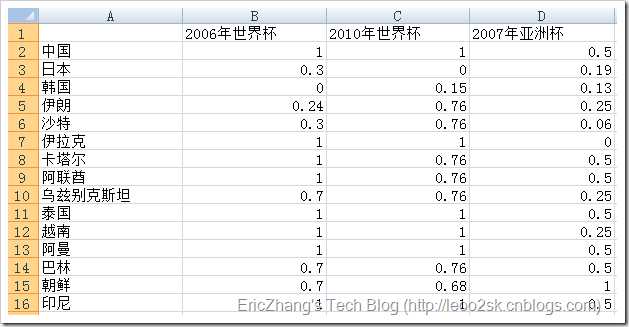
接着用k-means算法进行聚类。设k=3,即将这15支球队分成三个集团。
现抽取日本、巴林和泰国的值作为三个簇的种子,即初始化三个簇的中心为A:{0.3, 0, 0.19},B:{0.7, 0.76, 0.5}和C:{1, 1, 0.5}。下面,计算所有球队分别对三个中心点的相异度,这里以欧氏距离度量。下面是我用程序求取的结果:
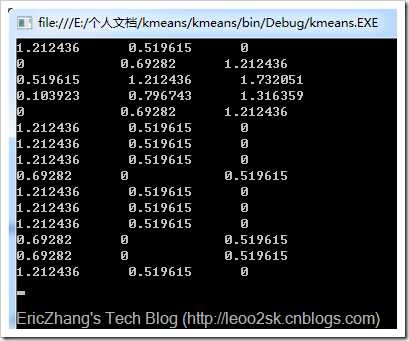
从做到右依次表示各支球队到当前中心点的欧氏距离,将每支球队分到最近的簇,可对各支球队做如下聚类:
中国C,日本A,韩国A,伊朗A,沙特A,伊拉克C,卡塔尔C,阿联酋C,乌兹别克斯坦B,泰国C,越南C,阿曼C,巴林B,朝鲜B,印尼C。
第一次聚类结果:
A:日本,韩国,伊朗,沙特;
B:乌兹别克斯坦,巴林,朝鲜;
C:中国,伊拉克,卡塔尔,阿联酋,泰国,越南,阿曼,印尼。
下面根据第一次聚类结果,调整各个簇的中心点。
A簇的新中心点为:{(0.3+0+0.24+0.3)/4=0.21, (0+0.15+0.76+0.76)/4=0.4175, (0.19+0.13+0.25+0.06)/4=0.1575} = {0.21, 0.4175, 0.1575}
用同样的方法计算得到B和C簇的新中心点分别为{0.7, 0.7333, 0.4167},{1, 0.94, 0.40625}。
用调整后的中心点再次进行聚类,得到:
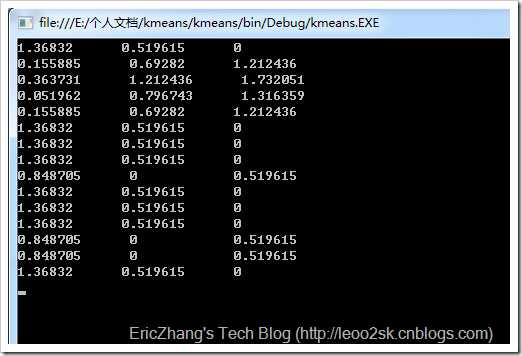
第二次迭代后的结果为:
中国C,日本A,韩国A,伊朗A,沙特A,伊拉克C,卡塔尔C,阿联酋C,乌兹别克斯坦B,泰国C,越南C,阿曼C,巴林B,朝鲜B,印尼C。
结果无变化,说明结果已收敛,于是给出最终聚类结果:
亚洲一流:日本,韩国,伊朗,沙特
亚洲二流:乌兹别克斯坦,巴林,朝鲜
亚洲三流:中国,伊拉克,卡塔尔,阿联酋,泰国,越南,阿曼,印尼
看来数据告诉我们,说国足近几年处在亚洲三流水平真的是没有冤枉他们,至少从国际杯赛战绩是这样的。
其实上面的分析数据不仅告诉了我们聚类信息,还提供了一些其它有趣的信息,例如从中可以定量分析出各个球队之间的差距,例如,在亚洲一流队伍中,日本与沙特水平最接近,而伊朗则相距他们较远,这也和近几年伊朗没落的实际相符。另外,乌兹别克斯坦和巴林虽然没有打进近两届世界杯,不过凭借预算赛和亚洲杯上的出色表现占据B组一席之地,而朝鲜由于打入了2010世界杯决赛圈而有幸进入B组,可是同样奇迹般夺得2007年亚洲杯的伊拉克却被分在三流,看来亚洲杯冠军的分量还不如打进世界杯决赛圈重啊。其它有趣的信息,有兴趣的朋友可以进一步挖掘。
源码下载:http://download.csdn.net/detail/lixiaolun/8666987
Similar to other algorithm, K-mean clustering has many weaknesses:
1 When the numbers of data are not so many, initial grouping will determine the cluster significantly. 当数据数量不是足够大时,初始化分组很大程度上决定了聚类,影响聚类结果。
2 The number of cluster, K, must be determined before hand. 要事先指定K的值。
3 We never know the real cluster, using the same data, if it is inputted in a different order may produce different cluster if the number of data is a few. 数据数量不多时,输入的数据的顺序不同会导致结果不同。
4 Sensitive to initial condition. Different initial condition may produce different result of cluster. The algorithm may be trapped in the local optimum. 对初始化条件敏感。
5 We never know which attribute contributes more to the grouping process since we assume that each attribute has the same weight. 无法确定哪个属性对聚类的贡献更大。
6 weakness of arithmetic mean is not robust to outliers. Very far data from the centroid may pull the centroid away from the real one. 使用算术平均值对outlier不鲁棒。
7 The result is circular cluster shape because based on distance. 因为基于距离,故结果是圆形的聚类形状。
One way to overcome those weaknesses is to use K-mean clustering only if there are available many data. To overcome outliers problem, we can use median instead of mean. 克服缺点的方法: 使用尽量多的数据;使用中位数代替均值来克服outlier的问题。
Some people pointed out that K means clustering cannot be used for other type of data rather than quantitative data. This is not true! See how you can use multivariate data up to n dimensions (even mixed data type) here. The key to use other type of dissimilarity is in the distance matrix.
转自:http://www.cnblogs.com/leoo2sk/archive/2010/09/20/k-means.html
&http://www.cnblogs.com/emanlee/archive/2012/03/06/2381617.html
标签:
原文地址:http://www.cnblogs.com/lixiaolun/p/4481280.html