标签:
canvas中绘制二次贝塞尔曲线的方法为ctx.quadraticCurveTo(x1,y1,x2,y2);
四个参数分别为两个控制点的坐标.开始点即当前canvas中目前的点,如果想从指定的点开始,需要使用ctx.moveTo(x,y)方法
演示效果如下图
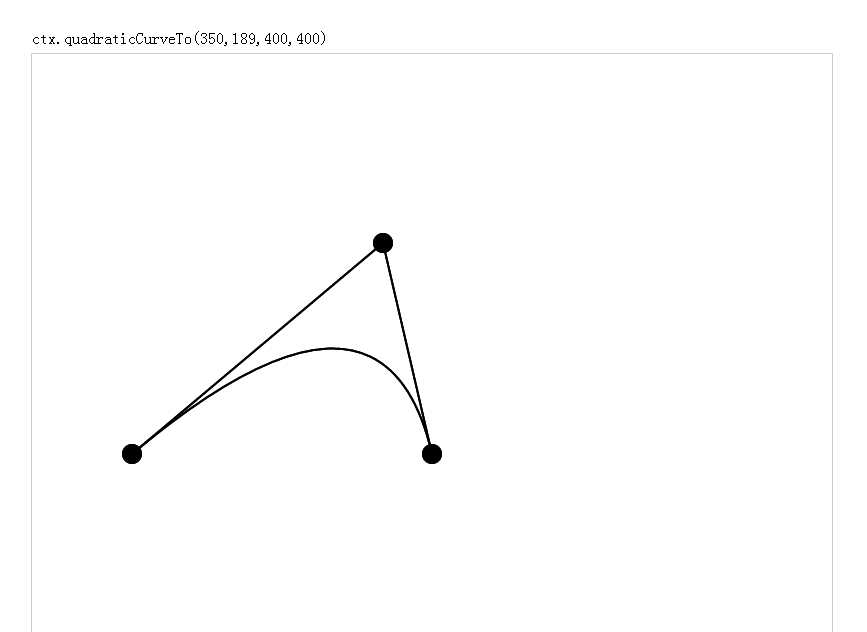
上代码:
html
<!doctype html>
<html>
<head>
<meta charset="utf-8">
<title>无标题文档</title>
<style>
*{ margin:0; padding:0;}
#info{ width:800px; height:30px; line-height:30px; margin:50px auto 0 auto;}
#canvas{ display:block; border:1px solid #ccc; margin:0px auto;}
</style>
<script src="js/dot.js"></script>
<script src="js/main.js"></script>
</head>
<body>
<div id="info"></div>
<canvas id="canvas" width="800" height="600"></canvas>
</body>
</html>
JS代码
dot.js
// JavaScript Document var dot = function ( x , y ){ this.x = x; this.y = y; this.r = dotR; } dot.prototype.draw = function (ctx){ ctx.save(); ctx.beginPath(); ctx.arc( this.x , this.y , this.r , 0 , Math.PI*2 ); ctx.fill(); ctx.closePath(); ctx.restore(); }
main.js
// JavaScript Document var CANVERS_WIDTH = 800; var CANVERS_HEIGHT = 600; var dotR = 10; var dotArr = []; window.onload = function(){ var oCanvas = document.querySelector("#canvas"); var oInfo = document.querySelector("#info"); var ctx = oCanvas.getContext("2d"); var dotA = new dot( 100 , 400 ); dotArr.push( dotA ); var dotB = new dot( 200 , 200 ); dotArr.push( dotB ); var dotC = new dot( 400 , 400 ); dotArr.push( dotC ); creatGuides(); createBezier(); function createBezier(){ ctx.save(); ctx.beginPath(); ctx.moveTo( dotA.x , dotA.y ); ctx.quadraticCurveTo( dotB.x , dotB.y , dotC.x , dotC.y ); ctx.stroke(); ctx.closePath(); ctx.restore(); } //绘制辅助线 ctx.lineWidth = 2; function creatGuides(){ dotA.draw( ctx ); dotB.draw( ctx ); dotC.draw( ctx ); ctx.save(); ctx.beginPath(); ctx.moveTo( dotA.x, dotA.y ); ctx.lineTo( dotB.x , dotB.y ); ctx.lineTo( dotC.x , dotC.y ); ctx.stroke(); ctx.closePath(); ctx.restore(); } oCanvas.onmousedown = function (e){ var disX = e.clientX - this.offsetLeft; var disY = e.clientY - this.offsetTop; //判断鼠标放下是是否在控制点上 var curDot = checkDot(disX,disY) if( curDot ){ if(oCanvas.setCapture){ oCanvas.setCapture(); } document.onmousemove = function (e){ oInfo.textContent ="ctx.quadraticCurveTo("+ dotB.x + "," + dotB.y + "," + dotC.x + "," + dotC.y + ")"; disX = e.clientX - oCanvas.offsetLeft; disY = e.clientY - oCanvas.offsetTop; curDot.x = disX; curDot.y = disY; console.log(disX) ctx.clearRect(0,0,CANVERS_WIDTH,CANVERS_HEIGHT); creatGuides(); createBezier(); } document.onmouseup = function (){ creatGuides(); createBezier(); document.onmousemove = null; document.onmouseup = null; if(oCanvas.setCapture){ oCanvas.releasesCaptrue(); } } return false; } } function checkDot(x,y){ for( var i=0; i<dotArr.length; i++ ){ if( Math.abs( dotArr[i].x - x ) < dotR && Math.abs( dotArr[i].y - y ) < dotR ){ return dotArr[i]; } } return false; } }
canvas绘制二次贝塞尔曲线----演示二次贝塞尔四个参数的作用
标签:
原文地址:http://www.cnblogs.com/liqingchang/p/4483661.html