A weighting function for ‘nls’/’nlsLM’

标签：

,http://www.r-bloggers.com/a-weighting-function-for-nls-nlslm/

           Standard nonlinear regression assumes homoscedastic(同方差的) data, that is , all response values yi are distributed normally. In case of heteroscedastic(异方差) data (i.e. when the variance is dependent on the magnitude of the data), weighting the fit is essential. In nls (or nlsLM of the minpack. Lm package), weighting can be conducted by two different methods:

(1). by supplying a vector of weighting values wi for every yi that is supplied to ‘weights‘ argument.

(2). by modifying the objective function in a way that it has the weights includes in the body of the function .An example is given for this one in the documentation to nls.

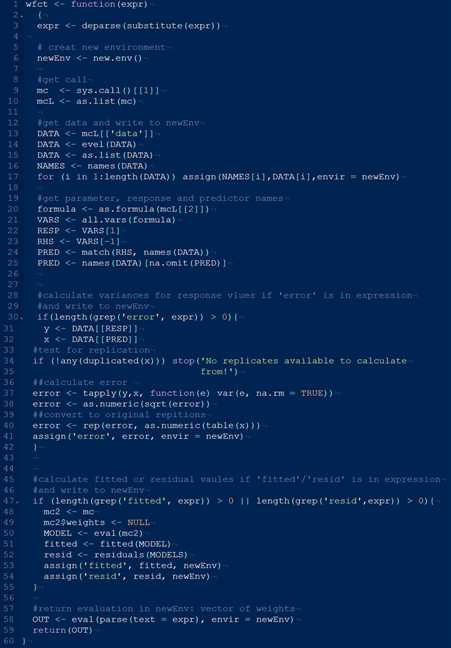
         Method (1) is easy of course, but all wi values have to be derived from somewhere, for example the reciproce(原文单词拼写错误) of the response values wi =1/yi. (2) is a bit more cumbersome and one dose not always want to define a new weighted version of the objective function. I found it about time to design a weighting function that can be supplied to the ‘weights‘ argument and that makes weighting by different regimes a breeze. wfct() returns a vector of weights that are calculated from a user-defined expression and transfers this vector within nls.

          The weighting function can take 5 different variable definitions and combinations thereof:

the name of the predictor(independent) variable;

the name of the response(dependent) variable;

error: if replicated yij exist, the error s(yij)；

fitted: the fitted values `yi of the model;

resid: the residuals yi-`yi of the model,

         For the last two, the model is fit unweight, fitted values and residuals are extracted and the model is refit by the defined weights.

         Let‘s have some example(take from the nls doc):

A common weighting regime is to use the inverse variance 1/ s²(y_i)

A weighting function for ‘nls’/’nlsLM’

标签：

原文地址：http://www.cnblogs.com/liulunyang/p/4486278.html