标签:
铺瓷砖的变种,做法也是类似
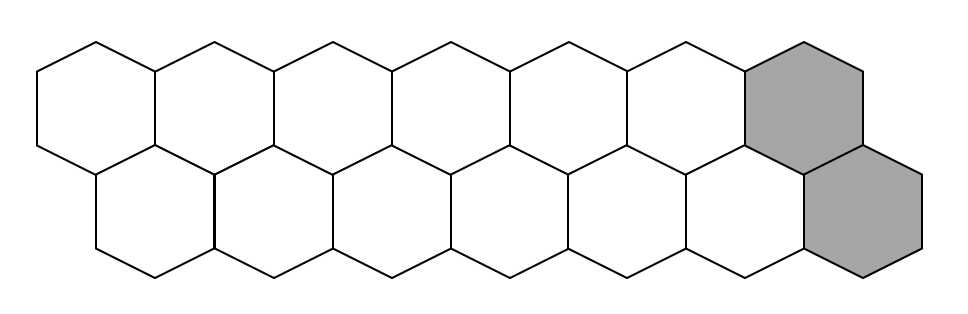
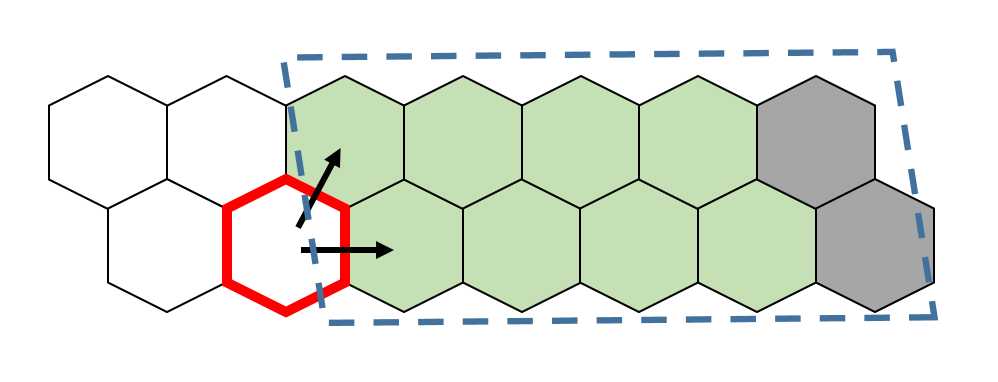
假设地板长下面这样,灰色的是无法填充的空洞,初始时可以把N块之外的地板填充成灰色的,便于边界处理
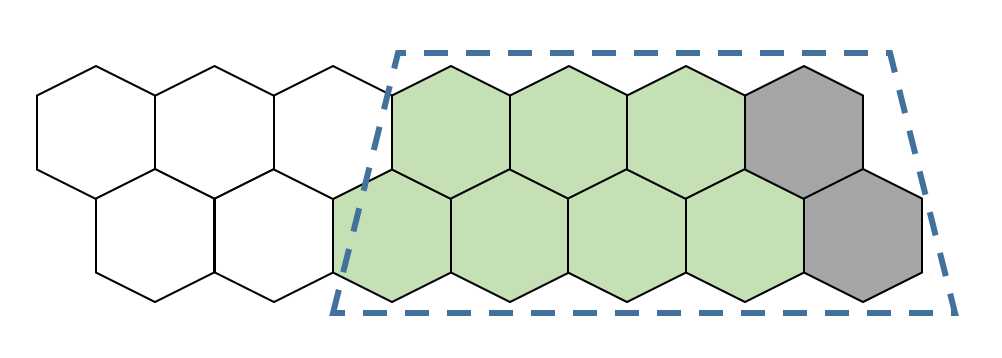
假设现在从后向前已经处理完了一部分,绿色的砖块代表已经遍历过了,蓝色虚线框代表已经计算完成的子问题
现在要遍历红色边框的地砖
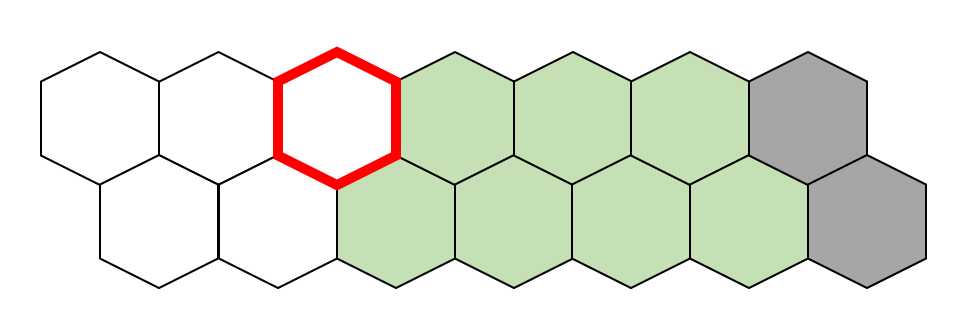
只可能有两种铺法:
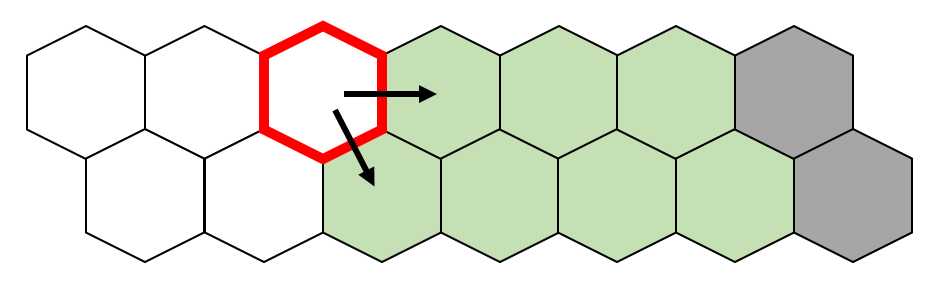
如果可以向下铺,很简单,递推到另一个子问题
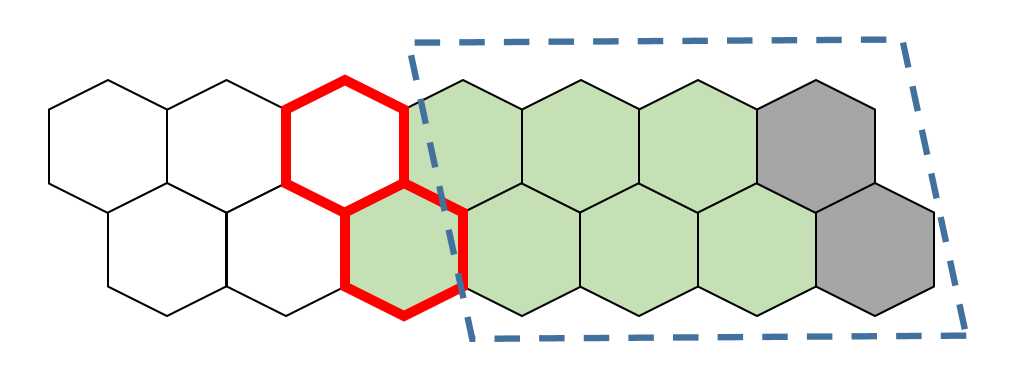
如果向右铺,就有些麻烦了,又两种可能
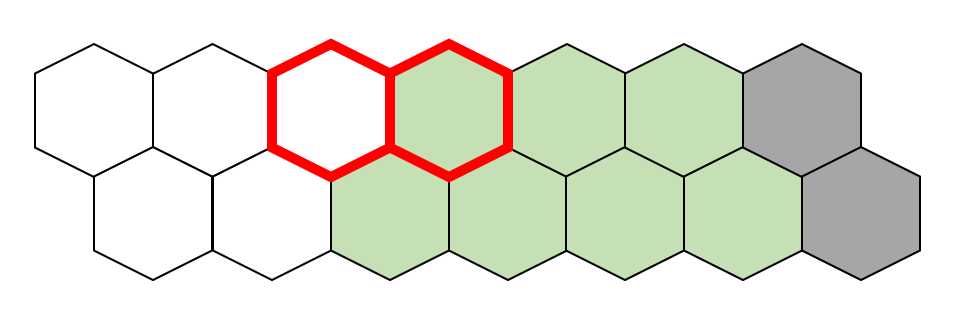
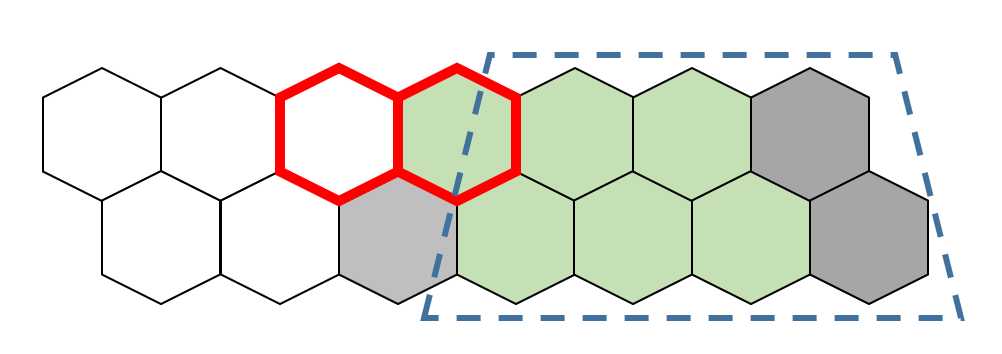
第一种可能,有块灰色的砖,如下图所示,则规约成一个子问题
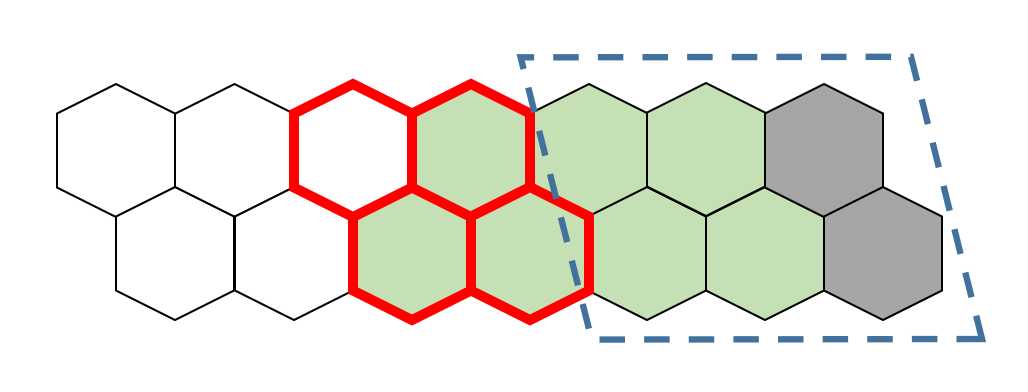
第二种可能,没有灰色的砖,下面也可以横着放,那么规约成另一个子问题
处理完这一步,就可以继续处理其他的砖了,也同样是类似的步骤
代码:
1 #include <cmath> 2 #include <cstdio> 3 #include <vector> 4 #include <iostream> 5 #include <algorithm> 6 #include <cstring> 7 using namespace std; 8 9 #define MAX_N 128 10 11 int N, T; 12 bool can[MAX_N][MAX_N]; 13 bool u[MAX_N]; 14 bool d[MAX_N]; 15 16 int main() { 17 /* Enter your code here. Read input from STDIN. Print output to STDOUT */ 18 cin >> T; 19 while (T--) { 20 cin >> N; 21 22 memset(u, 0, sizeof(u)); 23 memset(d, 0, sizeof(d)); 24 for (int i = 0; i < N; i++) { 25 char c; 26 cin >> c; 27 u[i] = c == ‘0‘ ? true : false; 28 } 29 for (int i = 0; i < N; i++) { 30 char c; 31 cin >> c; 32 d[i] = c == ‘0‘ ? true : false; 33 } 34 35 memset(can, 0, sizeof(can)); 36 for (int i = 0; i < 2; i++) 37 for (int j = 0; j < 2; j++) 38 can[N + i][N + j] = true; 39 40 int i = N; 41 int j = N; 42 while (i >= 0 || j >= 0) { 43 if (--j >= 0) { 44 if (!d[j]) { 45 can[i][j] = can[i][j + 1]; 46 } else { 47 if (u[i]) 48 can[i][j] |= can[i + 1][j + 1]; 49 if (d[j + 1]) { 50 if (!u[i]) 51 can[i][j] |= can[i + 1][j + 2]; 52 if (u[i] && u[i + 1]) 53 can[i][j] |= can[i + 2][j + 2]; 54 } 55 } 56 } 57 if (--i >= 0) { 58 if (!u[i]) { 59 can[i][j] = can[i + 1][j]; 60 } else { 61 if (d[j]) 62 can[i][j] |= can[i + 1][j + 1]; 63 if (u[i + 1]) { 64 if (!d[j]) 65 can[i][j] |= can[i + 2][j + 1]; 66 if (d[j] && d[j + 1]) 67 can[i][j] |= can[i + 2][j + 2]; 68 } 69 } 70 } 71 } 72 73 cout << (can[0][0] ? "YES" : "NO") << endl; 74 } 75 return 0; 76 }
标签:
原文地址:http://www.cnblogs.com/boring09/p/4493282.html