如果目标也已知的话,用双向BFS能很大提高速度
单向时,是 b^len的扩展。
双向的话,2*b^(len/2) 快了很多,特别是分支因子b较大时
至于实现上,网上有些做法是用两个队列,交替节点搜索 ×,如下面的伪代码:
while(!empty()){
扩展正向一个节点
遇到反向已经扩展的return
扩展反向一个节点
遇到正向已经扩展的return
}
但这种做法是有问题的,如下面的图:
求S-T的最短路,交替节点搜索(一次正向节点,一次反向节点)时
Step 1 : S –> 1 , 2
Step 2 : T –> 3 , 4
Step 3 : 1 –> 5
Step 4 : 3 –> 5 返回最短路为4,错误的,事实是3,S-2-4-T
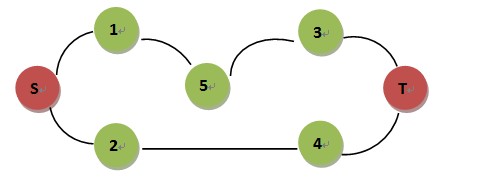
我想,正确做法的是交替逐层搜索,保证了不会先遇到非最优解就跳出,而是检查完该层所有节点,得到最优值。
也即如果该层搜索遇到了对方已经访问过的,那么已经搜索过的层数就是答案了,可以跳出了,以后不会更优的了。
当某一边队列空时就无解了。
优化:提供速度的关键在于使状态扩展得少一些,所以优先选择队列长度较少的去扩展,保持两边队列长度平衡。这比较适合于两边的扩展情况不同时,一边扩展得快,一边扩展得慢。如果两边扩展情况一样时,加了后效果不大,不过加了也没事。
无向图时,两边扩展情况类似。有向图时,注意反向的扩展是反过来的 x->y(如NOIP2002G2字串变换)
Time Limit:10000MS Memory Limit:65536K
Total Submit:28 Accepted:3
Case Time Limit:1000MS
Description
[问题描述]:
已知有两个字串 A$, B$ 及一组字串变换的规则(至多6个规则):
A1$ -> B1$
A2$ -> B2$
规则的含义为:在 A$中的子串 A1$ 可以变换为 B1$、A2$ 可以变换为 B2$ …。
例如:A$=‘abcd‘ B$=‘xyz‘
变换规则为:
‘abc’->‘xu’ ‘ud’->‘y’ ‘y’->‘yz’
则此时,A$ 可以经过一系列的变换变为 B$,其变换的过程为:
‘abcd’->‘xud’->‘xy’->‘xyz’
共进行了三次变换,使得 A$ 变换为B$。
Input
A$ B$
A1$ B1$ \
A2$ B2$ |-> 变换规则
... ... /
所有字符串长度的上限为 20。
Output
若在 10 步(包含 10步)以内能将 A$ 变换为 B$ ,则输出最少的变换步数;否则输出"NO ANSWER!"
Sample Input
abcd xyz
abc xu
ud y
y yz
Sample Output
3
Source
xinyue摘自NOIP2002提高组
转自:http://www.cppblog.com/xiongnanbin/articles/97899.html
分析:
双向BFS:
所谓双向搜索指的是搜索沿两个方向同时进行:
1.正向搜索:从初始结点向目标结点方向搜索。
2.逆向搜索:从目标结点向初始结点方向搜索。
当两个方向的搜索生成同一子结点时终止此搜索过程。
双向搜索通常有两种方法:
1. 两个方向交替扩展。
2. 选择结点个数较少的那个方向先扩展。
方法2克服了两方向结点的生成速度不平衡的状态,明显提高了效率。
- #include<iostream>
- using namespace std;
-
- struct node
- {
- char s[30];
- int dep;
- } list1[5010],list2[5010];
-
- char a[7][30],b[7][30];
- int n;
- bool check(char *s1,char *s2)
- {
- if (strlen(s1)!=strlen(s2)) return false;
- for (int i=0;i<strlen(s1);i++)
- if (s1[i]!=s2[i]) return false;
- return true;
- }
- bool pan1(char *s,int i,int x)
- {
- for (int j=i;j<i+strlen(a[x]);j++)
- if (s[j]!=a[x][j-i]) return false;
- return true;
- }
- bool pan2(char *s,int i,int x)
- {
- for (int j=i;j<i+strlen(b[x]);j++)
- if (s[j]!=b[x][j-i]) return false;
- return true;
- }
- void bfs()
- {
- int head1,tail1,head2,tail2,i,j,k,l;
- head1=tail1=head2=tail2=1;
-
- while (head1<=tail1 && head2<=tail2)
- {
- if (list1[head1].dep+list2[head2].dep>10)
- {
- printf("NO ANSWER!\n");
- return ;
- }
- for ( i=0;i<strlen(list1[head1].s);i++)
- for ( j=1;j<=n;j++)
- if (pan1(list1[head1].s,i,j))
- {
- tail1++;
- for (k=0;k<i;k++) list1[tail1].s[k]=list1[head1].s[k];
-
- for (l=0;l<strlen(b[j]);l++,k++) list1[tail1].s[k]=b[j][l];
-
- for (l=i+strlen(a[j]);l<=strlen(list1[head1].s);l++,k++)
- list1[tail1].s[k]=list1[head1].s[l];
-
- list1[tail1].s[k]=‘\0‘;
- list1[tail1].dep=list1[head1].dep+1;
-
- for (k=1;k<=tail2;k++)
- if (check(list1[tail1].s,list2[k].s))
- {
- printf("%d\n",list1[tail1].dep+list2[k].dep);
- return ;
- }
- }
-
- for ( i=0;i<strlen(list2[head2].s);i++)
- for ( j=1;j<=n;j++)
- if (pan2(list2[head2].s,i,j))
- {
- tail2++;
- for (k=0;k<i;k++) list2[tail2].s[k]=list2[head2].s[k];
- for ( l=0;l<strlen(a[j]);l++,k++) list2[tail2].s[k]=a[j][l];
- for (l=i+strlen(b[j]);l<=strlen(list2[head2].s);l++,k++)
- list2[tail2].s[k]=list2[head2].s[l];
- list2[tail2].s[k]=‘\0‘;
- list2[tail2].dep=list2[head2].dep+1;
- for (k=1;k<=tail1;k++)
- if (check(list1[k].s,list2[tail2].s))
- {
- printf("%d\n",list1[k].dep+list2[tail2].dep);
- return ;
- }
- }
- head1++; head2++;
- }
- printf("NO ANSWER!\n");
- }
-
- int main()
- {
-
- scanf("%s%s",list1[1].s,list2[1].s);
- n=1;
- while (scanf("%s%s",a[n],b[n])!=EOF) n++;
- n--;
- list1[1].dep=list2[1].dep=0;
- bfs();
- return 0;
- }

