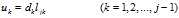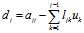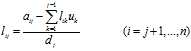由此,有时起始点选择很关键,如果函数只存在一个零点,那么这个起始点选取就无关重要。对已Logistic回归问题,Hessian矩阵对于任意数据都是负定的,所以说极值点只有一个,初始点的选取无关紧要。
-
using System;
-
using System.Collections.Generic;
-
using System.Text;
-
using Model.MatrixDecomposition;
-
using Model.Matrix;
-
using System.IO;
-
-
namespace Model.NewtonRaphson
-
{
-
internal class NewtonRaphsonIterate
-
{
-
Cholesky_LDL_Decomposition decompositionMatrixByLDL = new Cholesky_LDL_Decomposition();
-
-
private double[,] matrix_Hessian = null;
-
private double[,] matrix_X = null;
-
private double[,] matrix_A = null;
-
-
-
private double[,] vector_HU = null;
-
private double[,] vector_U = null;
-
private double[,] vector_Y = null;
-
private double[,] vector_Omega = null;
-
private double[,] vector_PI = null;
-
private double[,] old_VectorOmega = null;
-
-
#region 属性
-
public double[,] MatrixL
-
{
-
get
-
{
-
return decompositionMatrixByLDL.MatrixL;
-
}
-
}
-
-
-
public double[,] MatrixD
-
{
-
get
-
{
-
return decompositionMatrixByLDL.MatrixD;
-
}
-
}
-
-
public double[,] Hessian
-
{
-
get
-
{
-
return this.matrix_Hessian;
-
}
-
}
-
#endregion
-
-
/// <summary>
-
/// 执行牛顿迭代法
-
/// </summary>
-
/// <param name="matrix_X">输入矩阵</param>
-
/// <param name="vector_Y">输出向量</param>
-
/// <param name="error_Threashold">迭代停止阈值</param>
-
/// <param name="omega">计算完成的参数</param>
-
internal void Run(double[,] matrix_X, double[,] vector_Y, double error_Threashold, ref double[,] omega)
-
{
-
double error = 1;
-
this.matrix_X = matrix_X;
-
this.vector_Y = vector_Y;
-
this.vector_Omega = omega;
-
InitializeParameter(matrix_X.GetLength(0));
-
int i = 0;
-
while (error > error_Threashold)
-
{
-
i++;
-
error = 0;
-
old_VectorOmega = (double[,])vector_Omega.Clone();
-
GetMatrixAAndVectorPI();
-
matrix_Hessian = MatrixOperation.MultipleMatrix(
-
MatrixOperation.MatrixMultiDiagMatrix(
-
MatrixOperation.TransportMatrix(matrix_X), matrix_A),
-
matrix_X);
-
GetMatrixU();
-
decompositionMatrixByLDL.Cholesky((double[,])matrix_Hessian.Clone(), vector_U, ref vector_HU);
-
vector_Omega = MatrixOperation.AddMatrix(vector_Omega, vector_HU);
-
GetIterationError(ref error);
-
//TODO:迭代计算
-
}
-
omega = (double[,])vector_Omega.Clone();
-
}
-
-
private void InitializeParameter(int rowNumber)
-
{
-
matrix_A = new double[rowNumber, 1];
-
vector_PI = new double[rowNumber, 1];
-
}
-
-
/// <summary>
-
/// 获取H=X^TAX的A以及PI(Xi)
-
/// </summary>
-
private void GetMatrixAAndVectorPI()
-
{
-
for (int i = 0; i < matrix_X.GetLength(0); i++)
-
{
-
double temp_A = 0;
-
//matrix_A[i, 0] += vector_Omega[0, 0];
-
for (int j = 0; j < matrix_X.GetLength(1); j++)
-
{
-
temp_A += matrix_X[i, j] * vector_Omega[j, 0];
-
}//for2
-
matrix_A[i, 0] = (1.0) / (1 + Math.Exp(-temp_A));
-
vector_PI[i, 0] = matrix_A[i, 0];
-
matrix_A[i, 0] *= (1 - matrix_A[i, 0]);
-
-
}//for1
-
}
-
-
//计算HU中的U
-
//U=X^T(Y-PI)
-
private void GetMatrixU()
-
{
-
vector_U = MatrixOperation.MultipleMatrix(MatrixOperation.TransportMatrix(matrix_X),
-
MatrixOperation.SubtracteMatrix(vector_Y, vector_PI));
-
}
-
-
/// <summary>
-
/// 计算每次迭代完成后的误差
-
/// </summary>
-
/// <param name="error">误差</param>
-
private void GetIterationError(ref double error)
-
{
-
for (int i = 0; i < vector_Omega.GetLength(0); i++)
-
{
-
error += Math.Abs(vector_Omega[i, 0] - old_VectorOmega[i, 0]);
-
}
-
}
-
}
-
}
-
using System;
-
using System.Collections.Generic;
-
using System.Text;
-
using Model.Matrix;
-
-
namespace Model.MatrixDecomposition
-
{
-
internal class Cholesky_LDL_Decomposition
-
{
-
private double[,] matrix_L = null;
-
private double[,] matrix_D = null;
-
-
public double[,] MatrixL
-
{
-
get
-
{
-
return this.matrix_L;
-
}
-
}
-
-
-
public double[,] MatrixD
-
{
-
get
-
{
-
return this.matrix_D;
-
}
-
}
-
private int matrix_Dimension = 0;
-
-
#region Decomposition Matrix
-
/// <summary>
-
/// 方程AX=B
-
/// 利用Cholesky LDL^T分解法,求方程的解
-
/// </summary>
-
/// <param name="m_A">系数矩阵A</param>
-
/// <param name="v_B">列向量,B</param>
-
/// <param name="v_X">求得方程的解</param>
-
public void Cholesky(double[,] m_A, double[,] v_B, ref double[,] v_X)
-
{
-
this.matrix_Dimension = m_A.GetLength(0);
-
matrix_L = new double[matrix_Dimension, matrix_Dimension];
-
matrix_D = new double[matrix_Dimension, matrix_Dimension];
-
//为了计算方便,将L的严格下三角存储在A的对应位置上,
-
//而将D的对角元素存储A的对应对角位置上
-
//double[,] q = (double[,])m_A.Clone();
-
for (int i = 0; i < matrix_Dimension; i++)
-
{
-
for (int j = 0; j < i; j++)
-
{
-
m_A[i, i] -= m_A[j, j] * m_A[i, j] * m_A[i, j];
-
}//for
-
for (int k = i + 1; k < matrix_Dimension; k++)
-
{
-
for (int n = 0; n < i; n++)
-
{
-
m_A[k, i] -= m_A[k, n] * m_A[n, n] * m_A[i, n];
-
}//for
-
m_A[k, i] /= m_A[i, i];
-
}//for
-
}//for
-
-
this.GetLDMatrix(m_A);
-
this.SolveEquation(v_B,ref v_X);
-
//double[,] resut = MatrixOperation.MultipleMatrix(MatrixOperation.MultipleMatrix(MatrixL, MatrixD), MatrixOperation.TransportMatrix(MatrixL));
-
}
-
-
/// <summary>
-
/// 将L和D矩阵分别赋值
-
/// </summary>
-
/// <param name="m_A">经过Cholesky分解后的矩阵</param>
-
private void GetLDMatrix(double[,] m_A)
-
{
-
for (int i = 0; i < matrix_Dimension; i++)
-
{
-
matrix_L[i, i] = 1;
-
matrix_D[i, i] = m_A[i, i];
-
for (int j = 0; j < i; j++)
-
{
-
matrix_L[i, j] = m_A[i, j];
-
}
-
}
-
}
-
#endregion End Decomposition Matrix
-
-
#region Solve Equation
-
/// <summary>
-
/// 求解LY=B => Y
-
/// DL^TX=Y => X
-
/// </summary>
-
/// <param name="v_B">方程AX=B的列向量B</param>
-
/// <param name="v_X">求解结果</param>
-
private void SolveEquation(double[,] v_B, ref double[,] v_X)
-
{
-
v_X =(double[,])v_B.Clone();
-
//求解LY=B=>Y
-
for (int i = 0; i < matrix_Dimension; i++)
-
{
-
for (int j = 0; j < i; j++)
-
{
-
v_X[i,0] -= v_X[j,0] * matrix_L[i, j];
-
}
-
v_X[i,0] /= matrix_L[i, i];
-
}
-
-
//计算DL^T
-
double[,] dMultiLT = MatrixOperation.MultipleMatrix(matrix_D,
-
MatrixOperation.TransportMatrix(matrix_L));
-
//求解DL^TX=Y => X
-
for (int i = matrix_Dimension - 1; i >= 0; i--)
-
{
-
for (int j = i + 1; j < matrix_Dimension; j++)
-
{
-
v_X[i,0] -= v_X[j,0] * dMultiLT[i, j];
-
}
-
v_X[i,0] /= dMultiLT[i, i];
-
}
-
}//end Method
-
#endregion
-
}
-
}
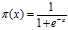
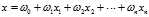
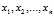 是输入变量的n个特征,然后按照Logistic函数形式求出。
是输入变量的n个特征,然后按照Logistic函数形式求出。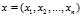 ,设条件概率
,设条件概率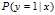 在x条件下y发生的概率(假设y=1为y发生)。则Logistic函数表示为:
在x条件下y发生的概率(假设y=1为y发生)。则Logistic函数表示为:
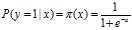
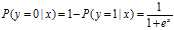
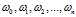 是Logistic回归模型的主要问题,采用的最大似然估计来求解这组参数。
是Logistic回归模型的主要问题,采用的最大似然估计来求解这组参数。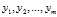 ,设
,设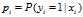 为给定条件下
为给定条件下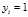 的概率,同理
的概率,同理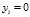 的概率为
的概率为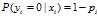 ,得到一个观测值得概率为:
,得到一个观测值得概率为:
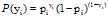

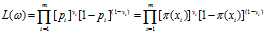

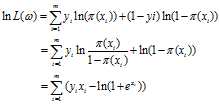
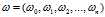 使的
使的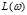 最大,其中:
最大,其中:
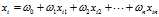
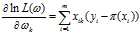
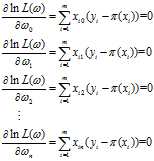
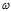 不一定是似然函数的极值,需要通过Hessian矩阵来判断得出的解是否为似然函数的极值。
不一定是似然函数的极值,需要通过Hessian矩阵来判断得出的解是否为似然函数的极值。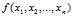 ,如果他的二阶偏导都存在,那么Hessian矩阵如下:
,如果他的二阶偏导都存在,那么Hessian矩阵如下: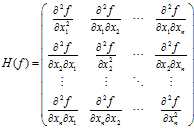
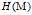 是正定矩阵,则临界点M处是一个局部极小值;
是正定矩阵,则临界点M处是一个局部极小值; 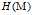 是负定矩阵,则临界点M处是一个局部极大值;
是负定矩阵,则临界点M处是一个局部极大值; 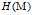 是不定矩阵,则临界点M处不是极值。
是不定矩阵,则临界点M处不是极值。 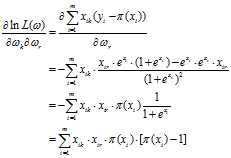
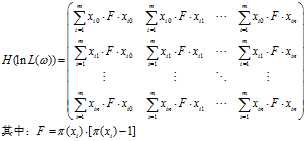
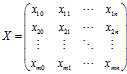
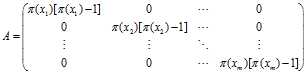
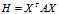
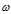 。
。 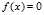 的解,首先选取一个点
的解,首先选取一个点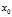 作为迭代起点,通过下面的式子进行迭代,直到达到指定精度为止。
作为迭代起点,通过下面的式子进行迭代,直到达到指定精度为止。 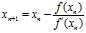

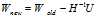
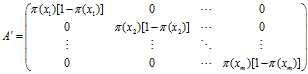
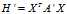
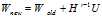
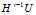 ,即解方程组
,即解方程组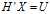 。由于
。由于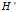 是对称正定的,可以使用Cholesky矩阵分解法来解。
是对称正定的,可以使用Cholesky矩阵分解法来解。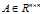 对称正定,则存在一个对角元为正数的下三角矩阵
对称正定,则存在一个对角元为正数的下三角矩阵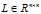 ,使得
,使得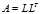 成立。对于
成立。对于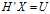 ,可以通过以下步骤求解:
,可以通过以下步骤求解: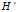 的Cholesky分解,得到
的Cholesky分解,得到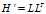
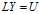 ,得到
,得到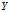
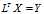 ,得到
,得到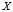
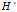 进行Cholesky分解。假设:
进行Cholesky分解。假设: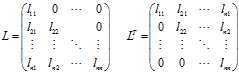
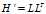 比较两边的关系,首先由
比较两边的关系,首先由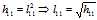
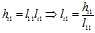
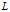 的第一列元素。假设,已经算出了
的第一列元素。假设,已经算出了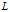 的前
的前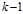 列元素,通过
列元素,通过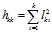

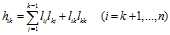
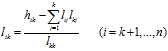
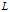 的前
的前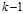 列求出了第
列求出了第 列,一直递推下去即可求出
列,一直递推下去即可求出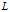 。这种方法称为平方根法。
。这种方法称为平方根法。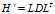
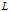 是单位下三角矩阵,
是单位下三角矩阵,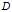 为对角均为正数的对角矩阵。把这一分解叫
为对角均为正数的对角矩阵。把这一分解叫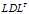 分解。设:
分解。设: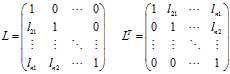
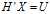 ,求解步骤变为:
,求解步骤变为: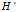 的
的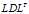 分解,得到
分解,得到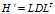
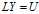 ,得到
,得到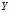
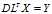 ,得到
,得到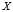
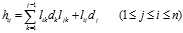
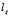 和
和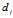 的公式如下:
的公式如下: