UVa1643 - Angle and Squares(几何)

标签：

有n个正方形和一个角(均在第一象限中)，使这些正方形与这个角构成封闭的阴影区域，求阴影区域面积的最大值。

分析：

直观上来看，当这n个正方形的对角线在一条直线上时，封闭区域的面积最大。(虽然我不太会证明，=_=||)

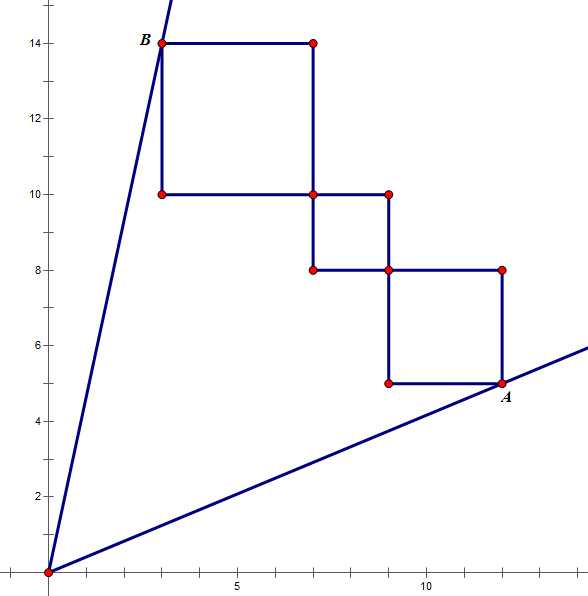
设所有正方形边长之和为L，OA、OB两直线方程分别为：y = k₁x  y = k₂x，设A(x₁, k₁x₁), B(x₂, k₂x₂)，可列出方程：

，解得，相应的就得到AB两点坐标，用叉积算出△OAB的面积再减去这些正方形面积的一半就是答案。

#include<cstdio>
#include<algorithm>
using namespace std;
struct Point{
    double x,y;
    Point(double x=0,double y=0):x(x),y(y){}
};
double Cross(const Point& A,const Point& B){
    return A.x*B.y-A.y*B.x;
}
int main()
{
    int n;
    while(scanf("%d",&n)&&n){
        Point A,B;
        double L=0,subArea=0,l;
        scanf("%lf%lf%lf%lf",&A.x,&A.y,&B.x,&B.y);
        for(int i=0;i<n;i++){
            scanf("%lf",&l);
            L+=l;
            subArea+=l*l/2;
        }
        double k1=A.y/A.x,k2=B.y/B.x;
        if(k1>k2) swap(k1,k2);
        double x1=(k1+1)*L/(k2-k1),y1=k1*x1;
        double x2=(k2+1)*L/(k2-k1),y2=k2*x2;
        A=Point(x1,y1),B=Point(x2,y2);
        double ans=Cross(A,B)/2-subArea;
        printf("%.3f\n",ans);
    }
    return 0;
}

UVa1643 - Angle and Squares(几何)

标签：

原文地址：http://blog.csdn.net/a197p/article/details/45670221