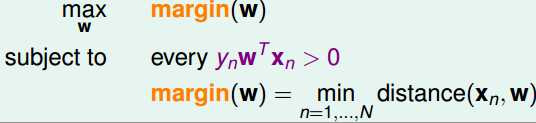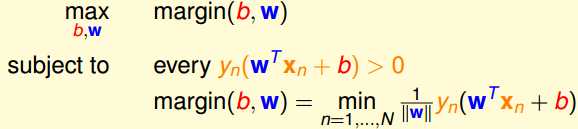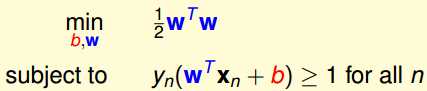标签:
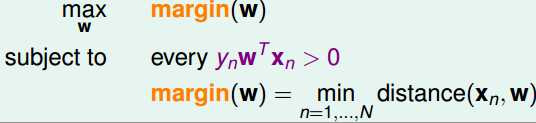
1.将公式中的distance具体化
将$w_0$单独抽出作为$b$,$w=(w_1,...,w_n),x=(x_1,...,x_n)$
则分割平面为:$w^Tx+b=0$
A.证明w为法向量
设两点$x‘,x‘‘$都在平面上,所以有
$w^Tx‘=w^Tx‘‘=-b$
$w^T(x‘-x‘‘)=0$
可以知道$x‘-x‘‘$是平面上的一个向量,$w$和它垂直,所以为法向量
B.距离表示为x-x‘到法向量的投影,同时使用第一个限制条件
$distance=|\frac{w^T(x-x‘)}{||w||}|=|\frac{w^Tx+b}{||w||}|=\frac{1}{||w||}y_n(w^Tx+b)$
2.使用放缩,简化条件
因为$w^Tx+b=0$和$3w^Tx+3b=0$表示同一个平面,适当放缩w和b
使 $\min\limits_{n=1,...,N} y_n(w^Tx+b) = 1$,则$margin(b,w)=\frac{1}{||w||}$
此时下方限制条件使最小的等于0,已经保证上方的条件,所以上方可省略
3.放松限制条件,去除min
A.变换条件,解不变
变条件为$y_n(w^Tx+b)\geq 1$
假设此时在$y_n(w^Tx+b)$上取得最优(b,w),
比如是在$y_n(w^Tx+b)=1.26$取得最优解,此时放缩(b,w)为$(\frac{b}{1.26},\frac{w}{1.26})$,
此时由于w变短,所以得到更好的解
因此,最优解不能在大于1的地方获得,最优解保持一致
B.变换max为min,并去除根号
1.2 linear SVM 推导
标签:
原文地址:http://www.cnblogs.com/porco/p/4501083.html