标签：dp   uva   

                             Steal the Treasure

The alliance of thieves decides to steal the treasure from country A. There are n cities in country A. Cities are connected by directional or bidirectional road. To avoid the risk, the king of country A divides his treasure and hides them in some place on the road.
  The alliance has found out the secret of the king. They get a map of country A which shows the location and the quantity of treasure on each road. In order to make the maximum profit and reduce the least loss, the alliance determines to send n thieves respectively to each city (one city one thief). At the appointed time, each thief chooses one road (if there is a road and notice that the road may have direction) to get to its corresponding city. Then he can steal the treasure on that road. After stealing, all the thieves return back to their base immediately.
  The heads of the alliance wonder to know the quantity of the treasure they can steal at most.

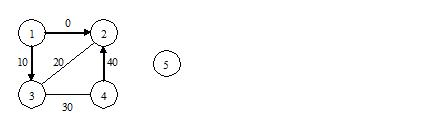
2 1
1 2 0 10
5 5
1 2 1 0
1 3 1 10
2 3 0 20
3 4 0 30
4 2 1 40

10
100

题意：有 n 个城市， m 条边，每条边连接两个城市。x y d w 表示，x y 之间有一条边，边上有财富值 w ，d 为 1 表示有向边， d 为 0 表示 无向边。小偷集团要窃取这些财富值，在每个 城市都有一个小偷，经过相邻的边时就会得到该条边对应的财富值。每条边只可以走一次。问最后可以得到的最大值。

思路：贪心，按边权从大到小排序。对于有向边，只能选起点，那无向边呢，两个点都是可以的，而且怎么选择对后面是有影响的。于是想到先把这两个点标记为待确定点，根绝后面的选择再确定这两个点。注意到一个点可能是多条无向边的端点，也就是说可能有许多点互相关联，待确定，只要其中有一个点被确定了，那么其他所有的点就都被确定好了。这样这些点构成了一个联通块，可以用并查集实现。这样贪心的时候，每个联通块缩为一个点，每个点的状态有已被选，和未选，再根据相应的策略去贪心就好了。

<span style="font-size:18px;">#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
#include <string>
#include <algorithm>
#include <queue>
#include <stack>
using namespace std;

const double PI = acos(-1.0);
const double e = 2.718281828459;
const double eps = 1e-8;
const int MAXN = 1010;
int father[MAXN];
struct Edge
{
    int u, v;
    int d, w;
} edge[MAXN*MAXN/2];
int vis[MAXN];
int n, m;

int Find(int x)
{   // 路径压缩
    return (x==father[x])?x:(father[x]=Find(father[x]));
}

int cmp(Edge a, Edge b)
{
    return a.w > b.w;
}

int main()
{
    //freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    while(cin>>n>>m)
    {
        for(int i = 1; i <= m; i++)
        {
            scanf("%d %d %d %d", &edge[i].u, &edge[i].v, &edge[i].d, &edge[i].w);
        }
        sort(edge+1, edge+1+m, cmp);
        for(int i = 1; i <= n; i++)
            father[i] = i;
        memset(vis, 0, sizeof(vis));
        int ans = 0;
        for(int i = 1; i <= m; i++)
        {
            int x = Find(edge[i].u);
            int y = Find(edge[i].v);
            if(vis[x] && vis[y])
                continue;
            if(edge[i].d==1 && vis[x])
                continue;
            ans += edge[i].w;
            if(edge[i].d == 1)
                vis[x] = 1;
            else
            {
                if(x == y)
                    vis[x] = 1;
                if(!vis[x] && !vis[y])
                    father[x] = y;
                else if(vis[x])
                    vis[y] = 1;
                else if(vis[y])
                    vis[x] = 1;
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}</span>

HDU 2480 - Steal the Treasure(贪心+并查集)

标签：dp   uva   

原文地址：http://blog.csdn.net/u014028317/article/details/45703115