想必大家都知道计算机内部是由 IC ①这种电子部件构成的。CPU(微处理器)和内存也是IC的一种。IC有几种不同的形状,有的像一条黑色蜈蚣,在其两侧有数个乃至数百个引脚;有的则像插花用的针盘,引脚在IC内部并排排列着。IC的所有引脚,只有直流电压0V或5V②两个状态。也就是说,IC的一个引脚,只能表示两个状态。
① IC是集成电路(Integrated Circuit)的简称,有模拟IC和数字IC两种。本章介绍的是数字IC。关于内存IC,我们会在第4章详细说明。② 大部分IC的电源电压都是+5V。不过,为了控制电量的消耗,有的IC也会使用+5V以下的电压。如果IC使用的电源电压为+5V,那么引脚状态就不只是0V和+5V,还存在不接收电流信号的高阻抗(high impedance)状态。但在本书中,我们暂时不考虑高阻抗状态。
IC的这个特性,决定了计算机的信息数据只能用二进制数来处理。由于1位(一个引脚)只能表示两个状态,所以二进制的计数方式就变成了0、1、10、11、100…这种形式。虽然二进制数并不是专门为IC而设计的,但是和IC的特性非常吻合(图2-1)。计算机处理信息的最小单位—— 位 ,就相当于二进制中的一位。位的英文bit是二进制数位(binary digit)的缩写。

二进制数的位数一般是8位、16位、32位……也就是8的倍数,这是因为计算机所处理的信息的基本单位是8位二进制数。8位二进制数被称为一个 字节 ①。字节是最基本的信息计量单位。位是最小单位,字节是基本单位。内存和磁盘都使用字节单位来存储和读写数据,使用位单位则无法读写数据。因此,字节是信息的基本单位。
① 字节是由bite(咬)一词而衍生出来的词语。8位(8 bit)二进制数,就类似于“咬下的一口”,因此被视为信息的基本单位。
用字节单位处理数据时,如果数字小于存储数据的字节数(= 二进制数的位数),那么高位上就用0填补。例如,100111这个6位二进制数,用8位(= 1字节)表示时为00100111,用16位(= 2字节)表示时为0000000000100111。奔腾等32位微处理器,具有32个引脚以用于信息的输入和输出。也就是说,奔腾一次可以处理32位(32位= 4字节)的二进制数信息。
程序中,即使是用十进制数和文字等记述信息,在编译后也会转换成二进制数的值,所以,程序运行时计算机内部处理的也是用二进制数表示的信息(图2-2)。
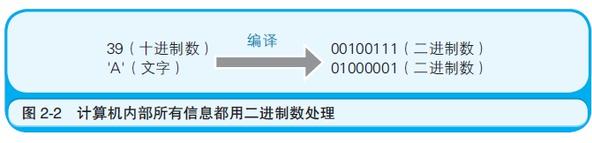
对于用二进制数表示的信息,计算机不会区分它是数值、文字,还是某种图片的模式等,而是根据编写程序的各位对计算机发出的指示来进行信息的处理(运算)。例如00100111这样的二进制数,既可以视为纯粹的数值作加法运算,也可以视为“‘”(单引号,single quotation)文字而显示在显示器上,或者视为■■□■■□□□这一图形模式印刷出来。具体进行何种处理,取决于程序的编写方式。
什么是二进制数?为了更清晰地说明二进制数的机制,首先让我们把00100111这个二进制数值转换成十进制数值来看一下。二进制数的值转换成十进制数的值,只需将二进制数的各数位的值和位权相乘,然后将相乘的结果相加即可(图2-3)。
假使有人问你:“为什么使用这样的转换方法呢?你能解释一下吗?”你这么回答是不行的:“不知道原因,只是把方法背下来了。”我们了解了二进制数的机制后,再看二进制数转换成十进制数的方法,就没有死记硬背的必要了。下面我们会对照着十进制数来说明二进制数的机制,这部分是重点,请大家一定要掌握。

首先,让我们从位权的含义说起。例如,十进制数39的各个数位的数值,并不只是简单的3和9,这点大家应该都知道。3表示的是3×10 = 30,9表示的是9×1 = 9。这里和各个数位的数值相乘的10和1,就是 位权。数字的位数不同,位权也不同。第1位(最右边的一位)是10的0次幂①(= 1),第2位是10的1次幂(= 10),第3位是10的2次幂(= 100),依此类推。这部分相信大家都能够理解。那么,我们就继续讲一下二进制数。
位权的思考方式也同样适用于二进制数。即第1位是2的0次幂(= 1),第2位是2的1次幂(= 2),第3位是2的2次幂(= 4),……,第8位是2的7次幂(= 128)。“○○的××次幂”表示位权,其中,十进制数的情况下○○部分为10,二进制数的情况下则为2。这个称为 基数 ②。十进制数是以10为基数的计数方法,二进制数则是以2为基数的计数方法。“○○的××次幂”中的××,在任何进制数中都是“数的位数-1”。即第1位是1- 1 = 0次幂,第2位是2- 1 = 1次幂,第3位是3- 1 = 2次幂。
① 所有数的0次幂都是1。② 数值的表现方法,进位计数制中各数位上可能有的数值的个数。十进制数的基数是10,二进制数的基数是2。
接下来,让我们来解释一下各数位的数值和位权相乘后“相加”这个处理的原因。其实大家所说的数值,表示的就是构成数值的各数位的数值和位权相乘后再相加的结果。例如39这个十进制数,表示的就是30+9,即各数位的数值和位权相乘后再相加的数值。
这种思考方式在二进制数中也是通用的。二进制数00100111用十进制数表示的话是39,因为(0×128)+(0×64)+(1×32)+(0×16)+(0×8)+(1×4)+(1×2)+(1×1) = 39。大家明白了吗?

本文摘自《程序是怎样跑起来的》
原文地址:http://blog.csdn.net/turingbooks/article/details/45746725