Decidability and R.E. Sets (II)

标签：

1. Listing Theorem

　　A non-empty set is r.e. iff it is the range of a unary total computable funciton.

　　That means the elements of a r.e. set can be effectively generated.

　　We can also prove that a set is r.e. iff it is the range of a computable function.

　　Corollary. Tot = {x | Φ_x is total} is not r.e.

　　Otherwise suppose Tot = Ran(f), where f is a total unary computable function, we can construct Φ_f(x)(X)+1, which differs from every unary computable function.

　　This proposition can also be proved by Rice-Shapiro Theorem, which will be introduced later.

　　Corollary. An infinite set is recursive iff it is the range of a total increasing computable function.

　　Corollary. An infinite r.e. set has an infinite recursive subset.

2. Rice-Shapiro Theorem

　　Suppose that A is a set of unary computable functions such that the set {x | Φ_x ∈ A} is r.e., then for any unary computable function f: f ∈ A iff there is a finite function θ ⊆ f with θ ∈ A . (The proof of this one is as hermetic as the previous version of Rice‘s Theorem in decidability.)

　　According to this theorem, following sets are not recursively enumerable:

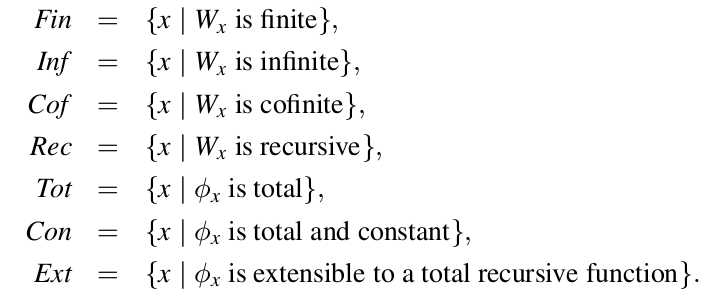
3. Special Sets

　　A set A is a productive set if there is a total computable function g such that whenever W_x⊆A, then g(x)∈ A\W_x. The function g is called a productive function for A. For example, the complement of K is productive with productive function g(x) = x.

　　Reduction Theorem.

　　Suppose that set A is productive, and there is a total computable function f such that x∈ A iff f(x)∈ B; then B is productive.

　　If β is a non-trivial set of unary computable functions who contains f_Φ, then the set {x|Φ_x∈β} is productive.

　　A set A is creative if it is r.e. and its complement is productive.

　　Suppose α is a set of unary computable functions and let A = {x|Φ_x∈α}; if A is r.e but neither empty nor N, then A is creative.

　　Subset Theorem.

　　A productive set must contain an infinite r.e. subset, which can be proved by construction based on the following lemma:

　　For any total computable function g, there is a total computable function k such that for all x, W_k(x) = W_x U {g(x)}.

　　A simple set is an r.e. set whose complement is infinite but does nnot contain infinite r.e. subset.

　　A simple set can never be recursive or creative.

　　We can prove that simple sets exist by constructing Ran(φ_x(μz(φ_x(z) > 2x))).

=========================================================

　　染指江湖皆悲剧，无人逃得过宿命。

Decidability and R.E. Sets (II)

标签：

原文地址：http://www.cnblogs.com/DevinZ/p/4506821.html