Matlab模拟双点光源干涉

标签：

一. 数学模型

设空间两定点S1、S2在同一介质中向一切方向发出两个相同频率的这样的波,振源振动可表示为
E01=A1Cos(ωt+?01)
E02=A2Cos(ωt+?02)
若用r1,r2分别表示任意空间的观察点P到点光源S1,S2的距离,当两列波达到P点时,振动可以表达为
E1=A1Cos(ωt+?01?kr1)
E2=A2Cos(ωt+?02?kr2)
其中 k=2π/λ,
假定两束光在空间任意点P的偏振方向一致,则在P点上两束光的叠加强度为:

二. Matalb 代码

function dbpiont(dd,Lamda,A,B,C,D)
%%
% 参数: A,B,C,D 像平面 Ax+By+Cz+D=0
%       dd: 光源距离
%       Lambda: 光波长
% dbpiont(2,0.0006328,1,-10,0,1000)
%%
axis([-10 10 -10 10 -10 10]);
grid on
x1 = dd/2;
x2 = -dd/2;
y1=0;y2=0;
z1=0;z2=0;  %确定点光源位置   
L=200;      %观察窗口 LxL平面
x=linspace(-10,10,L);%确定观察窗口的大小和位置
y=x;
NCLevels=256;
[X,Y]=meshgrid(x,y);%创建L@L个点阵的平面
%根据输入的平面Ax+By+Cz+D=0的参数A、B、C、D,确定平面上与观察窗口对应部分的L@L个点阵平面的三维坐标
if A==0 & B==0
    Z=(-D/C)*ones(L);
else if B==0 & C==0
        Z=X;
        X=(-D/A)*ones(L);
    else if A==0 & C==0
            Z=Y;
            Y=(-D/B)*ones(L);
        else    if C==0
                    Z=Y;
                    Y=(-D-X.*A)./B;
                else
                    Z=(-D-X.*A-Y.*B)./C;
            end
        end
    end
end
%计算点阵平面任意点到两光源的距离差并存储于一个L@L矩阵中
for i=1:L
  for j=1:L
    d1=sqrt((X(i,j)-x1)^2+(Y(i,j)-y1)^2+(Z(i,j)-z1)^2);
    d2=sqrt((X(i,j)-x2)^2+(Y(i,j)-y2)^2+(Z(i,j)-z2)^2);
    d(i,j)=d2-d1;
  end
end
%计算平面上各点的光强
I=cos((d.*pi)./Lamda).^2;
colormap(gray(NCLevels));
Ir=I.*NCLevels;
%绘制给定平面干涉条纹的图形
mesh(X,Y,Z,Ir)
hold on
%绘制点光源
plot3(x1,y1,z1,‘r.‘);
plot3(x2,y2,z2,‘r.‘);

两光源取在x轴上关于原点对称相距为2mm,波长K=63218nm,平面为-x-10g+1000=0,观察窗口宽度为20X20

dbpiont(2,0.0006328,1,-10,0,1000)

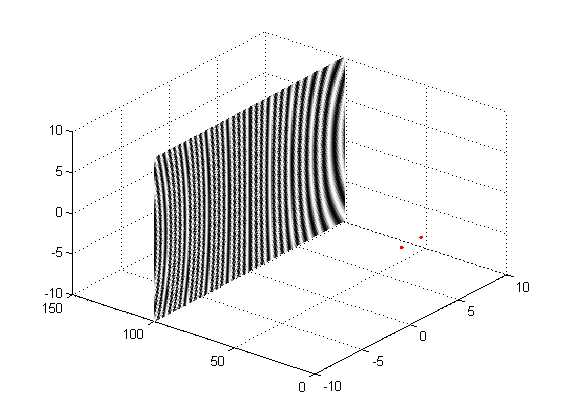
可以看出平面中间部分为等间距干涉条纹,两边为弧形条纹;

若取平面x=250mm时得到一组同心圆条纹。

dbpiont(2,0.0006328,1,0,0,-250)

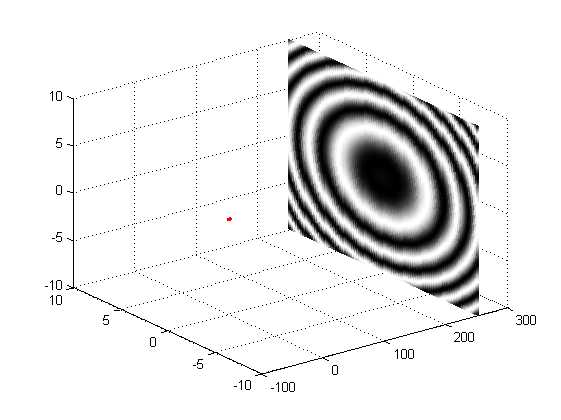
如果改变输入参数即任意改变平面的位置,及改变观察窗口的位置和大小,将得到三维空间任意位置的干涉图

三. 进一步讨论

若考虑双点光源发射的是球面光波,光场各处的光强随着传播距离增大而变小,则程序中光强计算式为

Matlab模拟双点光源干涉

标签：

原文地址：http://www.cnblogs.com/crossmind/p/4519534.html