hihocoder #1042 : 跑马圈地

标签：hihocoder   c++   

描述

一觉醒来，小Hi穿越回了古代！由于破敌有功，大汗赏赐小Hi可以在敌人的草原上跑马圈地：一天之内骑马围住的草原以后就是小Hi的牧场。但是令小Hi头疼的是，敌人的草原上有一块臭水塘。小Hi不能骑马走进臭水塘里，并且即使小Hi的骑马路径围住了臭水塘，小Hi的牛马也不能在臭水塘里放牧。

为了更科学地圈地，小Hi对这个问题进行了简化和抽象：(1)敌人的草原是一块n×m的方格矩阵，(2)骑马的路径是沿着方格边缘的一段封闭折线，(3)臭水塘是矩阵中的一块矩形，(4)骑马的路径周长不超过L。小Hi想知道自己最大能圈住多大面积的草原(臭水塘的面积不计入在内)。

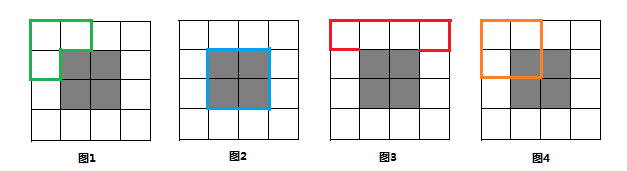
如图所示：图1是一条合法的路径；图2也是一条合法的路径，但是圈住的草原面积为0；图3不是合法的路径，因为没有封闭；图4也不是合法的路径，因为穿过了水塘。

输入

第一行3个整数：n, m, L (1 <= n, m <= 100, 1 <= L <= 400)

第二行4个整数：l, r, t, b (0 <= l < r <= m, 0 <= t < b <= n)表示水塘的左、右、上、下边界坐标。

输出

小Hi最大能圈住的面积

样例输入

4 4 8
1 3 1 3

样例输出

3

很显然L越大覆盖的面积就越大，所以这题应该是周长取L时枚举所有的面积。

主要是考虑一下三种情况：

1.圈地与水塘没有重叠部分

2.水塘的一个顶点在圈地内

3.水塘的四个顶点都在圈地内

可以通过坐标变换，把水塘都变成位于草原右上角的情况。

根据水塘中心的坐标来判断水塘是位于左上、右上、左下还是右下。

对于水塘坐标的转换

int l1, r1, t1, b1;
	if (l + r <= m &&t + b <= n)   //左下角
	{
		l1 = m - r;
		r1 = m - l;
		t1 = n - b;
		b1 = n - t;
	}
	else if (l + r >= m &&t + b <= n)  //右下角
	{
		l1 = l;
		r1 = r;
		t1 = n - b;
		b1 = n - t;
	}
	else if (l + r <= m &&t + b >= n)  //左上角
	{
		l1 = m - r;
		r1 = m - l;
		t1 = t;
		b1 = b;
	}

int l1, r1, t1, b1;
	l1 = l;
	r1 = r;
	t1 = t;
	b1 = b;
	if (l + r <= m)   
	{
		l1 = m - r;
		r1 = m - l;
	}
	if (t + b <= n)
	{
		t1 = n - b;
		b1 = n - t;
	}

#include <iostream>
using namespace std;

int main()
{
	int n, m, L, l, r, t, b;
	cin >> n >> m >> L;
	cin >> l >> r >> b >> t;
	if (L >= 2 * (m + n))
	{
		cout << m*n - (r - l)*(t - b) << endl;
		return 0;
	}
	int l1, r1, t1, b1;
	l1 = l;
	r1 = r;
	t1 = t;
	b1 = b;
	if (l + r <= m)   
	{
		l1 = m - r;
		r1 = m - l;
	}
	if (t + b <= n)
	{
		t1 = n - b;
		b1 = n - t;
	}
	int ans = 0;
	for (int i = 1; i < L / 2 && i <= m; i++)
	{
		for (int j = 1; j <= L / 2 - i&&j <= n; j++)
		{
			if (i <= l1 || j <= b1)
				ans = ans >i*j ? ans : i*j;
			else if (i > l1 && i <= r1 && j > b1 && j <= t1)
				ans = ans > i*j - (i - l1)*(j - b1) ? ans : i*j - (i - l1)*(j - b1);
			else if (i >= r1&&j >= t1)
				ans = ans > i*j - (r - l)*(t - b) ? ans : i*j - (r - l)*(t - b);
			else
				continue;
		}
	}

	cout << ans << endl;
	system("pause");

	return 0;
}

(づ￣ 3￣)づ

hihocoder #1042 : 跑马圈地

标签：hihocoder   c++   

原文地址：http://blog.csdn.net/youb11/article/details/45895431