标签:
题目输入一些结点,要求建立一颗二叉树,这些结点输入方式方式是(value, pos),value代表一个正int型的数,pos是一个仅由L与R组成的字符串,L代表左子树,R代表右子树,LRR代表root(根结点)的左子树的左子树的右子树的根结点,此结点的值即为value。
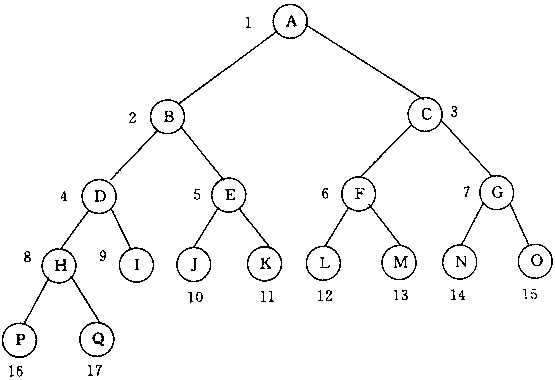
思路:采用一个map来保存结点值,map类型为mp <int, int> 前一个int为当前结点的位置,这个位置类似于满二叉树的位置表示法,像下图一样。之所以不用数组,是因为不大能确定数组的大小,题目只说了结点数最多为256个,但并不以位置pos最大为256。map中后一个int表示该结点的值。
每一个输入一个结点时,用sscanf方法获取值,用strchr方法获取含有位置信息的字符串,在map里添加结点的同时需要判断这个结点是否被输入了两次,因为被输入两次是不符合题目要求的。
/*
UvaOJ 122
Emerald
Thu 21 May 2015
*/
#include <iostream>
#include <cstring>
#include <cstdio>
#include <string>
#include <queue>
#include <map>
using namespace std;
const int MAXN = 512 + 8;
int counter = 0;
// int treeNode[ MAXN + 10 ];
map < int, int > treeNode; // map < position, value >
bool isOkay = true;
void Init() { // the initialization
// memset( treeNode, -1, sizeof(treeNode) );
treeNode.clear();
counter = 0;
isOkay = true;
}
void AddTreeNode( const string &s ) { // add a new node to the BT
int value = 0;
int i;
for( i=1; i<s.length() && s[i]!=‘,‘; i ++ ) {
value = value*10 + s[i] - ‘0‘;
}
int pos = 1;
i ++;
while( i<s.length() && s[i]!=‘)‘ ) {
if( s[i ++] == ‘L‘ ) {
pos = pos * 2;
} else {
pos = pos * 2 + 1;
}
}
if( treeNode.count( pos ) ) {
isOkay = false;
return ;
}
treeNode[ pos ] = value;
counter ++;
return ;
}
bool isComplete() { // according to the tree, is the tree complete ?
if( !treeNode.count( 1 ) ) {
return false;
}
queue <int> q; // queue <position>
q.push( 1 );
int linkAmount = 0;
while( ! q.empty() ) {
int t = q.front();
q.pop();
linkAmount ++;
if( treeNode.count( t*2 ) ) {
q.push( t*2 );
}
if( treeNode.count( t*2 + 1) ) {
q.push( t*2+1 );
}
}
return counter == linkAmount;
}
void PrintTree() { // print the tree as the problem requires
printf( "%d", treeNode[1] );
map < int, int > :: iterator it = treeNode.begin();
for( it++; it!=treeNode.end(); it ++ ) {
printf( " %d", it->second );
}
printf("\n");
}
int main() {
string in;
Init();
while( cin >> in ) {
if( in == "()" ) {
if( !isOkay || !isComplete() ) {
printf("not complete\n");
} else {
PrintTree();
}
Init();
} else {
AddTreeNode( in );
}
}
return 0;
}
标签:
原文地址:http://www.cnblogs.com/Emerald/p/4520861.html