标签:
1- M - P 模型
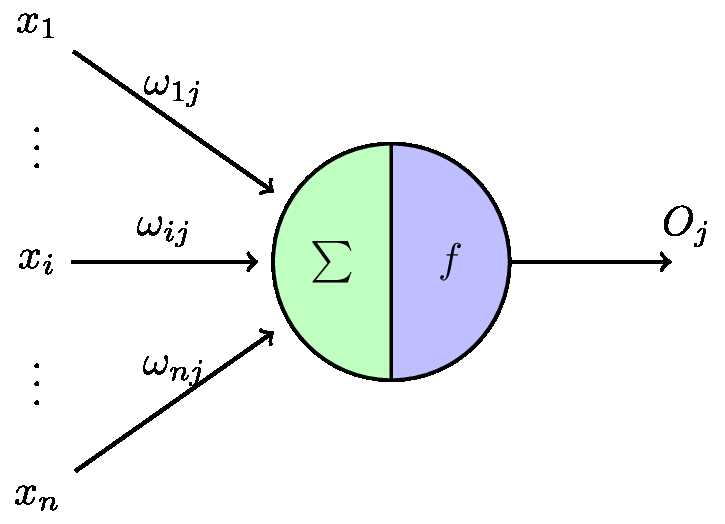
按照生物神经元,我们建立M-P模型。为了使得建模更加简单,以便于进行形式化表达,我们忽略时间整合作用、不应期等复杂因素,并把神经元的突触时延和强度当成常数。右图就是一个M-P模型的示意图。
那么接下来就好类比理解了。我们将这个模型和生物神经元的特性列表来比较:

结合M-P模型示意图来看,对于某一个神经元 $j$ (注意别混淆成变量了,在这里 $j$ 只是起到标识某个神经元的作用),它可能接受同时接受了许多个输入信号,用 $\chi_i$ 表示,前面说过,由于生物神经元具有不同的突触性质和突触强度,所以对神经元的影响不同,我们用权值 $\omega_{ij}$ 来表示,其正负模拟了生物神经元中突出的兴奋和抑制,其大小则代表了突出的不同连接强度。由于累加性,我们对全部输入信号进行累加整合,相当于生物神经元中的膜电位,其值就为:\[\begin{equation}net_{j}^{‘}=\sum_{i=1}^{n}\omega_{ij}\chi_{i}\end{equation}\]
神经元激活与否取决于某一阈值电位,即只有当其输入总和超过阈值 $T_{j}$ 时,神经元才被激活而发放脉冲,否则神经元不会发生输出信号。整个过程可以用下面这个函数来表示:\[\begin{equation}\omicron_{j}=f\big\{\small[\sum_{i=1}^{n}\omega_{ij}\chi_{i}\small]-T_{j}\big\}\end{equation}\]
如果 $\chi_{0}=-1, \omega_{0j}=T_{j}$,则有 $-T_{j}=\chi_{0}\omega_{0j}$。上述公式可以简化为:\[\begin{align}&net_{j}^{‘}=W_{j}^{T}X\\&\omicron_{j}=f(net_{j})=f(W_{j}^{T}X)\end{align}\]
2- 感知器
在1958年,美国心理学家Frank Rosenblatt提出一种具有单层计算单元的神经网络,称为感知器(Perceptron)。它其实就是基于M-P模型的结构。我们可以看看它的拓扑结构图。
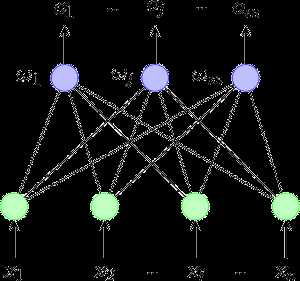
这个结构非常简单,其实就是输入输出两层神经元之间的简单连接。
我们一般采用符号函数来当作单层感知器的传递函数,即输出\[\begin{equation}\omicron_{j}=sgn(net_{j}^{‘}-T_{j})=sgn(\sum_{i=0}^{n}\omega_{ij}x_{i})=sgn(W_{j}^{T}X)\end{equation}\]
公式(5)可以进一步表达为:
\[\omicron_{j}=\left\{ \begin{array}{rr}-1,\quad W_{j}^{T}X>0\\1,\quad W_{j}^{T}X<0\end{array}\right.\]
2.1 单层感知器的局限性
虽然单层感知器简单而优雅,但它显然不够聪明——它仅对线性问题具有分类能力。什么是线性问题呢?简单来讲,就是用一条直线可分的图形。比如,逻辑“与”和逻辑“或”就是线性问题,我们可以用一条直线来分隔0和1。
A. 逻辑“与”的真值表和二维样本图如图:
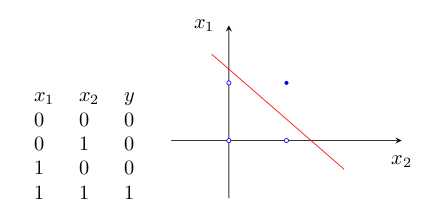
B. 逻辑“或”的真值表如图:
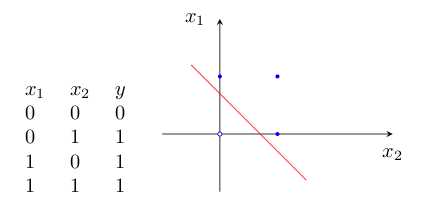
为什么感知器就可以解决线性问题呢?这是由它的传递函数决定的。这里以两个输入分量 $x_{1}$ 和 $x_{2}$ 组成的二维空间为例,方程$$\omega_{1j}x{1}+\omega{2j}x_{2}-T_{j}=0$$确定的直线就是二维输入样本空间上的一条分界线。
3- BP算法
标签:
原文地址:http://www.cnblogs.com/freyr/p/4522350.html