hihocoder #1083 : 积分

标签：c++   hihocoder   几何重心   

描述

在平面上有一个顶点数为N的多边形P，区域

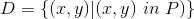
你需要写一个程序计算这个积分

输入

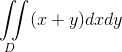
输入包含T (T<=500)个测试用例。数字T在输入文件的第一行给出。每个测试用例的第一行是一个整数N代表多边形的点数。其后跟随N行，每行包含两个点Xi和Yi，表示第i个点的坐标，当我们以给定的顺序连接这些点，我们得到了一个多边形。题目保证多边形不自交，这个多边形的面积也不会是零，也不会出现3个相邻的点共线的情况。

【参数说明】

3 <= N <= 8000

|Xi|, |Yi| <= 20000

输出

对于每个测试用例行输出结果占一行。将答案四舍五入到小数点后两位（0.005四舍五入到0.01）。

样例输入

2
4
4 -1
-1 4
-6 -1
-1 -6
4
0 0
10 0
10 10
0 10

样例输出

-100.00
1000.00

为了做这题逼得我把积分看了一下，想到上次做微积分还是很久远的事情。

知道怎么求任意凸多边形的重心么~链接拿好http://wenku.baidu.com/view/1e0c290bf78a6529647d53f2.html

概括一下怎么求重心：

在物理中重心的求法是：

在数学上密度是均匀的，所以密度函数可以看成常量，约去后得到：

而且

发现题目要求的东西可以变成这样：

对于无规则的凸多边形，以某个固定的顶点向其他顶点划线，可以把这个凸多边形分成多个三角形的组合。

然后这个题目就分解成了求多个三角形的重心坐标以及三角形的面积。

利用三角形个顶点坐标求解三角形面积的办法：叉乘

面积为S=|CA向量叉乘CB向量|/2=|(x2-x1)*(y3-y1)-(y2-x1)*(x3-x1)|/2

#include <iomanip>
#include <iostream>
using namespace std;

double x[8005], y[8005];

int main() 
{
	int T, n;
	cin >> T;
	while(T--) 
	{
		cin >> n;
		for (int i = 0; i < n;i++)
			cin >> x[i] >> y[i];

		double ans = 0;
		double small_s;
		double S = 0;
		for (int i = 2; i < n; i++)
		{
			small_s = ((x[i - 1] - x[0])*(y[i] - y[0]) - (y[i - 1] - y[0])*(x[i] - x[0])) / 2.0;
			S += small_s;
			double xg = (x[i - 1] + x[0] + x[i]) / 3.0;
			double yg = (y[i - 1] + y[0] + y[i]) / 3.0;
			ans += (xg + yg)*small_s;
		}
		if (S < 0)
			ans = -ans;
		
		cout << fixed << setprecision(2) << ans << endl;
	}
	
	system("pause");
	return 0;
}

hihocoder #1083 : 积分

标签：c++   hihocoder   几何重心   

原文地址：http://blog.csdn.net/youb11/article/details/45919249