标签:
浮点数在计算机中的存储方式遵循IEEE754标准。
IEEE754标准建立于1985年,80年代起所有的计算机系统均支持IEEE754。
IEEE754定义了32位单精度和64位双精度两种浮点二进制小数标准。
IEEE754用二进制科学记数法来表示浮点数。
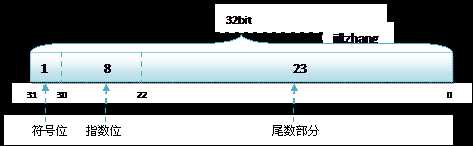
32位单精度浮点数,float,占用4Byte,32bit,用1位表示数字的符号,用8位来表示指数,用23位来表示尾数。
SEEEEEEE EMMMMMMM MMMMMMMM MMMMMMMM
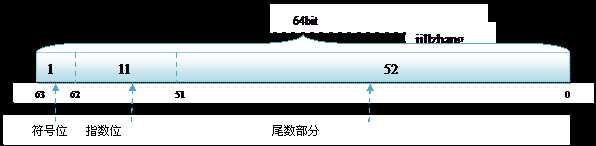
64位双精度浮点数,double,占用8Byte,64bit,用1位表示数字的符号,用11位表示指数,52位表示尾数。
SEEEEEEE EEEEMMMM MMMMMMMM MMMMMMMM MMMMMMMM MMMMMMMM MMMMMMMM MMMMMMMM
1.符号位(Sign):有正负之分,1代表负,0代表正
2.指数位(Exponent):用于存储科学计数法中的指数数据,并且采用移码表示。32位单精度浮点数中,指数位为十进制指数加上127后的值的二进制数。能表示的指数范围为-127-128,移码为+127,内存中数值范围为0-255。64位双精度浮点数移码为+1023。
3.尾数部分(Mantissa):即底数部分,用二进制小数表示。原码表示。因为二进制科学计数法小数部分第一位都是1,将小数点前面的1省略。32位单精度浮点数,23bit的尾数部分,可以表示的精度是24bit。因为9的二进制表示为1001,所以4bit能精确十进制中的1位小数点,24bit就能使float精确到小数点后6位。
注意:这里有个特例,浮点数为0时,指数和底数都为0,但此前的公式不成立。因为2的0次方为1,所以,0是个特例。当然,这个特例编译器会自动去识别。
另外:指数位采用移码可以实现快速比较两个浮点数的大小,例如:
1.0×2^-1 不使用移码时表示为:0 11111111 00000000000000000000000 十六进制为:0x7F800000
1.0×2^1 不使用移码时表示为:0 00000001 00000000000000000000000 十六进制为:0x00800000
比较得出的结果是错误的。
1.0×2^-1 使用移码时表示为:0 01111110 00000000000000000000 十六进制:0x3F000000
1.0×2^1 使用移码时表示为:0 10000000 00000000000000000000 十六进制:0x40000000
这样的话,就可以得出正确结果了。
例子:
1、十进制转换为float。将17.625换算成 float型
首先,将17.625换算成二进制:10001.101。再将10001.101向左移,直到小数点前只剩一位。1.0001101 x 2^4
尾数部分,为0001101
指数部分,实际为4,加上127,为131,即10000011
符号部分,由于是正数,所以为0
所以,17.625的float存储格式就是:0 10000011 00011010000000000000000 16进制:0x 41 8D 00 00
2、float转换为十进制。
二进制:11000001 01001000 00000000 00000000 十六进制:0x C1 48 00 00
符号部分:为1,是个负数。
指数部分:为10000010。转为10进制为130,130-127=3,即实际指数部分为3
尾数部分:为10010000000000000000000。在尾数数左边省略存储了一个1,使用实际底数表示为1.10010000000000000000000
现在将科学计数法还原。可以通过指数部分E的值来调整底数部分M的值。这里,E为正3,得: 1100.10000000000000000000
小数点左边的1100表示为 (1 × 23) + (1 × 22) + (0 × 21) + (0 × 20),其结果为12
小数点右边的 .100… 表示为 (1 × 2-1) + (0 × 2-2) + (0 × 2-3) + ... ,其结果为.5
以上二值的和为12.5, 由于S为1,是负数,即-12.5
Java中浮点数的具体特性(转载自码农合作社)
JVM中的浮点数的尾数用2进制数表示。规范化的二进制数小数点出现在非0最高有效位前面。由于二进制数系统只有2个数字,1和0,所以最高有效位上的数字总是1。
在JVM中,浮点数的指数位可以指明该数是不是一个规范化浮点数。如果指数位全0,则为非规范化数,最高有效位肯定是0。其他情况下,则为规范化浮点数,最高有效位肯定是1。
在JVM中,任何浮点运算都不会抛出异常。类似除数为0的问题操作,JVM会返回一些特殊值,比如正/负无穷,或NaN(不是一个数)。尾数位全是0的情况下,如果指数位全是1,符号位是0,则表示正无穷;如果指数位位全是1,符号位是1,则表示负无穷。如果指数位全是1,尾数位不全是0,则表示NaN。JVM总是为NaN使用相同的尾数:最高有效位是1,其他全为0。
| Special float values | Float bits (sign exponent mantissa) |
| +Infinity | 0 11111111 00000000000000000000000 |
| -Infinity | 1 11111111 00000000000000000000000 |
| NaN | 1 11111111 10000000000000000000000 |
非全0和非全1的指数位表示规范化尾数要乘以的2的幂数。可以把阶码当做一个正数,然后减去一个偏移量,这样就能得到实际的幂数。对float数来说,偏移量是126;而double数,则为1023。例如,一个float数的阶码为00000001,则幂数为-125(1 – 126),这是float中最小的幂数。再看一个例子,如果阶码是11111110,则幂数为128(254 – 126),这是float中最大的幂数。
| Normalized float values | Float bits (sign exponent mantissa) | Unbiased exponent |
| Largest positive (finite) float | 0 11111110 11111111111111111111111 | 128 |
| Largest negative (finite) float | 1 11111110 11111111111111111111111 | 128 |
| Smallest normalized float | 1 00000001 00000000000000000000000 | -125 |
| Pi | 0 10000000 10010010000111111011011 | 2 |
指数位全0,说明尾数没有规范化,也隐含说明了最高有效为是0,而不是1。这种情况下,幂数为浮点数的最小幂数。对float来说,是-125。这意味着,规范化尾数乘以2 -125的浮点数,它的阶码为00000001,而非规范化尾数乘以2 -125的浮点数,它的阶码为00000000。阶码范围底端的非规范化数修正值,使得下溢出较为平缓。如果最小阶码用来表示规范化数,下溢成0的最小数值会更大一些。 换句话说,让最小阶码表示非规范化数,可以使浮点数能表示更小的数值。虽然非规范化数的精度没有规范化数高,但是,这相对于阶码一旦达到最小规范化数值,浮点数就会下溢成0来说,非规范化数更好一些。
| Denormalized float values | Float bits (sign exponent mantissa) |
| Smallest positive (non-zero) float | 0 00000000 00000000000000000000001 |
| Smallest negative (non-zero) float | 1 00000000 00000000000000000000001 |
| Largest denormalized float | 1 00000000 11111111111111111111111 |
| Positive zero | 0 00000000 00000000000000000000000 |
| Negative zero | 1 00000000 00000000000000000000000 |
标签:
原文地址:http://www.cnblogs.com/yuexiaohao/p/4523684.html