标签:
题目链接:点击打开链接
祭出结论:点击打开链接
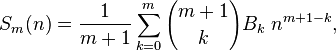
资料:组合数回代公式:点击打开链接
伯努利数:点击打开链接
方法一:
首先给出一个神奇的组合数公式: C(n,k)+C(n+1,k)+C(n+2,k)+C(n+3,k)……+C(N,k)
由于: C(n,k)=C(n-1,k)+C(n-1,k-1)
因此 上式 = - C(n,k+1) + { C(n,k+1)+C(n,k) } + C(n+1,k)……
= - C(n,k+1) + {C(n+1,k+1} + C(n+1,k)…… (发现性质了么??,C(n+1,k+1)又与C(n+1,k)结合)
= - C(n,k+1)+ C(N+1,k+1)
现在我们来看如何利用上面这种性质:
对于: i^k 我们写成 F(i)= i*(i+1)*(i+2)……*(i+k-1)=C(i+k-1,k)
如果我们把右边的式子展开: i^k + t1 * i^(k-1) ……+ tk-1 * i , 如果我们知道i^p(p<k)的公式 ,那么合并在一起就可以得到i^k的公式了
设S(k)表示1^k+2^k+3^k……+n^k的和,那么:
F(1)+F(2)+F(3)……+F(n)
=C(1+k-1,k)+C(2+k-1,k)……+C(n+k-1,k)
= C(n+k,k+1)
= S(k) + t1 * S(k-1) + t2 * S(k-2) …… + tk-1 * S(1) 则可以得到S(k)的表达式
方法二:
对于1^k+2^k+3^k……+n^k 必然能写成多项式:t1 * n^(k+1) +
t2 * n^k …… 根据这个多项式,我们可以利用高斯消元来求出ti的值 ,由于ti不一定为整数,这里貌似就只能用分数来实现了。
方法三:
设F(K,N) = 1^N+2^N+3^N+4^N+5^N+...+K^N.
我们要讨论的是在O(N^2)时间限制内能求出上式对于任意K的值.
如一般所知,
F(K,1) = (K+1)*K/2
以及N=2时的通式.
那么当N=3,4,5..呢?
下面是求解过程.
假定已经求得了N-1, N-2,...1的通式.
那么对于N,设K固定,表达式简化为Fn
(K+1)^(N+1) = K^(N+1) + C(N,1)*K^N + C(N,2)*K^(N-1) + ... + C(N,N)
K^(N+1) = (K-1)^(N+1) + C(N,1)*(K-1)^N + C(N,2)*(K-1)^(N-1) + ... + C(N,N)
... ...
1^(N+1) = 1^N
上面的K+1个式子,分别将等号右边的第一项移位到等号左边.
(K+1)^(N+1) - K^(N+1) = C(N,1)*K^N + C(N,2)*K^(N-1) + ... + C(N,N)
K^(N+1) - (K-1)^(N+1) = C(N,1)*(K-1)^N + C(N,2)*(K-1)^(N-1) + ... + C(N,N)
... ...
1^(N+1) - 1^N = 0
左边累加和 = (K+1)^(N+1) - 1,
右边累加和 = C(N,1)*Fn+C(N,2)F(n-1)+ ... + C(N,N)F0
左边=右边,则
Fn=((K+1)^(N+1)-(C(N,2)F(n-1)+ ... + C(N,N)F0 + 1)) / N
得证.
1^k+2^k+3^k+··· ZOJ 3547 UVA 766
标签:
原文地址:http://blog.csdn.net/qq574857122/article/details/45937711