标签:
扩展kmp:
用于求串的各个后缀与原串的最长公共前缀的长度;
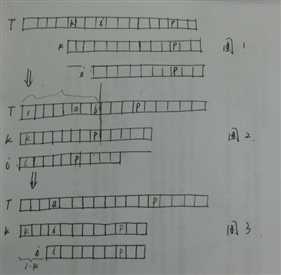
上图的是字符串自匹配的过程:
图一:
假设现在匹配到i-1了,开始求next [ i ] 的值,此时,k记录的是到目前为止匹配到的最远的位置的那一次的起点,p标志的是已经匹配过的最远的点;
图二:
因为前面是匹配过的,所以可以知道,k~p和源串的1~b是一模一样的,所以 i 匹配的前一段可以和k~p段直接匹配,而不用和源串匹配,如果i匹配完成后,从i开始next[ i ]长度是和源串一模一样的。这个时候可以看图三。
图三:
可以看到 i 与 k 的相对位置和a 与 1 的相对位置是一样的,而且1~a与k~i之间的是一样的,i与a也是一样的,而且next[ a ]是已经计算过的,所以用l = next[ i - k ]
p=k+next[ k ]; 然后 if ( l<p)就是当用之前的匹配结果没有匹配超出p那么就可以直接用之前的结果了:next[ i ]=l;如果超出了p的范围,就要把超出的部分匹配一下,然后要更新k;
这样自匹配就结束了;
然后是字符间匹配,过程几乎一模一样;不再详述;
代码如下;

1 /* 2 扩展kmp,计算小串对于大串的每一个后缀的最大公共前缀; 3 这里求a串关于b串的每个后缀的最长公共前缀; 4 首先是a串自匹配; 5 然后串间匹配; 6 */ 7 #include<iostream> 8 #include<cstdio> 9 #include<cstring> 10 #include<string> 11 #include<algorithm> 12 using namespace std; 13 string a,b; 14 int next[10000]={0},ret[100000]={0}; 15 int m,n; 16 void extended_kmp() 17 { 18 //next[]数组记录的是自匹配的长度; 19 //ret[]数组记录的是字符串之间匹配的长度; 20 //a是子串,b是长串; 21 int i,j,k; 22 for(j=0;j+1<m&&a[j]==a[j+1];j++); 23 next[1]=j; 24 k=1; //k表示的是最远的匹配到的那一个子串的起点; 25 for(i=2;i<m;i++) 26 { 27 int p=k+next[k],l=next[i-k]; //len记录的是目前匹配到的最远的位置; 28 if(l<p-i) 29 next[i]=l; 30 else 31 { 32 for(j=max(0,len-i);i+j<m&&a[j]==a[i+j];j++); 33 next[i]=j; 34 k=i; 35 } 36 } 37 for(j=0;j<n&&j<m&&a[j]==b[j];j++); 38 ret[0]=j; 39 k=0; 40 for(i=1;i<n;i++) 41 { 42 int p=k+next[k],l=next[i-k]; 43 if(l<p-i) 44 ret[i]=l; 45 else 46 { 47 for(j=max(0,len-i);j<m&&i+j<n&&a[j]==b[i+j];j++); 48 ret[i]=j; 49 k=i; 50 } 51 } 52 } 53 int main() 54 { 55 cin>>a>>b; 56 m=a.size(); 57 n=b.size(); 58 extended_kmp(); 59 return 0; 60 }
标签:
原文地址:http://www.cnblogs.com/by-1075324834/p/4525743.html