标签:
一般来说,线性可分的训练数据的分界超平面往往并不唯一,但不同的超平面对于测试的识别效果却仍有差别。SVM是通过使超平面在每一个方向上与每一类各自最近的店距离相同从而达到最优线性分类效果。除此之外,SVM在求解超平面的过程中,还能够通过构造核函数使得非线性可分的数据变得线性可分。
在用SVM法构造出目标函数(其中m为样本数)
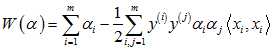
和限制条件
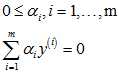
后,可以通过SMO法求解。
SMO法求解多变量目标函数的思想是,只将目标函数中的两个变量作为输入变量,而将其余的所有变量暂时看作参变量,再用梯度下降法或牛顿法或者解析法求解最优的两个输入变量,并根据此思路依次求解其他的两个变量,直到求解出所有的最优变量值,并得到收敛目标函数值。
详细原理可参考http://www.cnblogs.com/jerrylead/archive/2011/03/13/1982639.html
下图为SVM算法流程图,绿色为SVM参数训练流程,红色为具体样本分类流程。
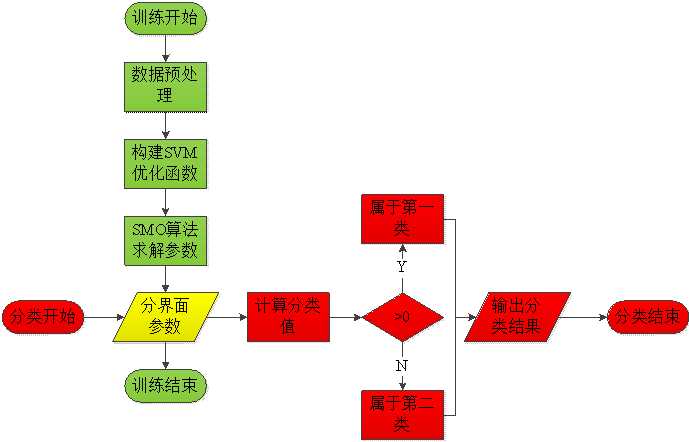
SVM算法流程图
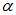 初始化等。实验数据为已修改的可先行可分的50个数据,其中40个作为训练数据,剩余十个作为测试数据。
初始化等。实验数据为已修改的可先行可分的50个数据,其中40个作为训练数据,剩余十个作为测试数据。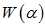 中,得到目标函数
中,得到目标函数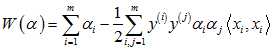 ;
;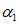 和
和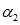 和参数变量
和参数变量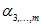 ;然后给参数变量
;然后给参数变量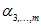 赋值得到关于输入变量的二元一次方程
赋值得到关于输入变量的二元一次方程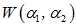 ,代入限制条件
,代入限制条件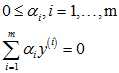 求解输入变量
求解输入变量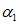
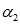 ,并更新
,并更新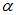 中的
中的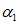
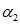 ;
;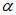 中选择不同的
中选择不同的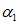
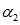 重复第3步,直到更新所有
重复第3步,直到更新所有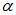 ;
;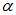 中所有的值是否满足限制条件,假如不满足,设置为目标函数的变量,重复第3步,直到
中所有的值是否满足限制条件,假如不满足,设置为目标函数的变量,重复第3步,直到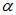 中所有的值都满足限制条件。
中所有的值都满足限制条件。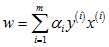 ,
,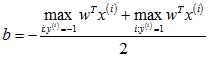 ;
;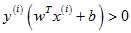 则分类正确,否则分类错误,统计分类正确率。测试数据为包括50个训练数据的3000个数据样本。
则分类正确,否则分类错误,统计分类正确率。测试数据为包括50个训练数据的3000个数据样本。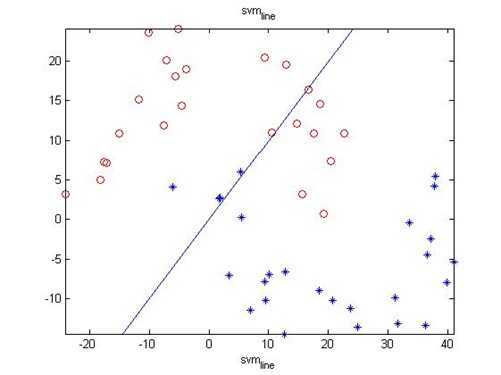
非线性可分数的SVM分类效果图
由分类图各标签点的分布可知,该训练数据并不是线性可分的。实验结果分析,一方面,对于每一次循环,不同的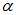 初始化对于最后的分类效果并没有很大影响;另一方面,循环数目的增加并没有提升分类效果。(我感觉是训练样本的非线性可分性造成的影响。)
初始化对于最后的分类效果并没有很大影响;另一方面,循环数目的增加并没有提升分类效果。(我感觉是训练样本的非线性可分性造成的影响。)
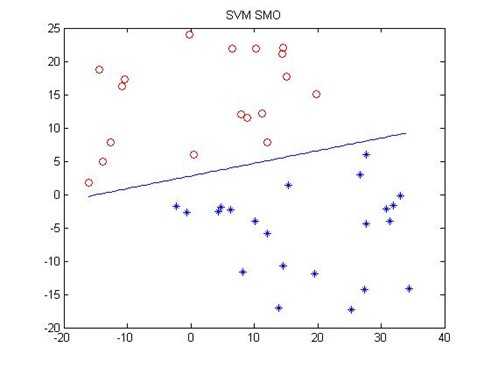
线性可分数的SVM分类效果图
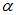 ,构造了多输入变量目标函数
,构造了多输入变量目标函数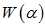 ,当多输入训练样本数特别大时,MATLAB无法对目标函数
,当多输入训练样本数特别大时,MATLAB无法对目标函数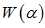 进行相关计算。
进行相关计算。在使用不带有效核函数的SVM法对非线性可分数据分类情况下,SMO法每次求解目标函数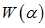 时的两个变量时发现,求解到的
时的两个变量时发现,求解到的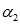 一般都偏向于0,使得
一般都偏向于0,使得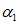 存在少量较小的负值。而这些负的
存在少量较小的负值。而这些负的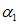 使得最后的求解结果并不满足KKT条件,从而导致实验结果的不理想。
使得最后的求解结果并不满足KKT条件,从而导致实验结果的不理想。
附MATLAB程序,包含两个m文件,主程序PRSVM.m,生产多变量向量的函数文件vecvariable.m,求解多变量优化函数的SMO算法。SVM线性可分实验数据可在http://pan.baidu.com/s/1ntIHhbF下载:
主程序
%2015.5.20 by anchor
%SVM solved by smo
clc;clear all;close all;
%============== PART 1: Data Preprocessing ============
dataset = load (‘dataset.mat‘);
data = dataset.dataset;
dataset = data(:,1:40);
[data_l,data_n] = size(dataset);
for data_n_i=1:data_n
if dataset(3,data_n_i) == -1
plot(dataset(1,data_n_i),dataset(2,data_n_i),‘*‘);
else
plot(dataset(1,data_n_i),dataset(2,data_n_i),‘ro‘);
end
hold on;
end
title(‘SVM SMO‘);
ylabel = dataset(3,:)‘;
dataset = dataset(1:2,:);
%========= PART 2: Solve Dual Problem With SMO ========
alpha_p = my_smo(dataset,ylabel);
% caculate parameters,omega and b
omega_p = dataset*(alpha_p.*ylabel);
coord_n1 = find(ylabel == -1);
coord_p1 = find(ylabel == 1);
b_p = -1/2*(max(omega_p‘*dataset(:,coord_n1))+min(omega_p‘*dataset(:,coord_p1)));
%===================== PART 3: Testing ======================
TestLabel = data(3,41:50);
TestData = data(1:2,41:50);
[TestData_l,TestData_n] = size(TestData);
correct = 0;
for input_n = 1:TestData_n
y_out = (omega_p‘*TestData(:,input_n)+b_p);
if TestLabel(input_n)*y_out>=0
correct =correct+1;
end
end
x=min(dataset(1,:)):0.5:max(dataset(1,:))
y=-omega_p(1)/omega_p(2)*x-b_p/omega_p(2);
plot(x,y)
fprintf(‘The correct rate of classification testing is %.2f %% \n‘,correct/TestData_n*100);
vecvariable.m
%2015.5.10 by anchor
%generate a vec_l dimensional variable vector
function vector=vecvariable(vector_l)
syms variable_name1;
vector=variable_name1;
for i=2:vector_l
syms ([‘variable_name‘,num2str(i)]);
vector=[vector;[‘variable_name‘,num2str(i)]];
end
end
my_smo.m
%function smo to solve multiple variables optimization problems
%2015.5.20 by anchor
function alpha_p=my_smo(dataset,ylabel)
data_n = length(ylabel);
XY_matrix = ylabel*ylabel‘.*(dataset‘*dataset);
alpha_p= 0.1*rand(data_n,1);
limit_c =0.5;
for iteration=1:2
for smo_n = 1:2:data_n
ylabel_temp =ylabel;
ylabel_temp(smo_n:smo_n+1) = [];
alpha_p_v = vecvariable(data_n); %define alpha variables vector
alpha_p_v_temp =alpha_p_v;
alpha_p_v_temp(smo_n:smo_n+1) = [];
alpha_p_temp = alpha_p;
alpha_p_temp(smo_n:smo_n+1) = [];
W_alpha = sum(alpha_p_v)-1/2*alpha_p_v‘*XY_matrix*alpha_p_v;%objective function
l_alpha_p_temp =length(alpha_p_temp);
for i =1:l_alpha_p_temp
W_alpha = subs(W_alpha,alpha_p_v_temp(i),alpha_p_temp(i));
end
W_alpha = subs(W_alpha,-ylabel(smo_n)*(ylabel(smo_n+1)*alpha_p_v(smo_n+1)+alpha_p_temp‘*ylabel_temp));
diff_W_alpha = diff(W_alpha,alpha_p_v(smo_n+1));
alpha_p(smo_n+1) = solve(‘diff_W_alpha=0‘);
if alpha_p(smo_n+1) < 0
alpha_p(smo_n+1) = 0;
elseif alpha_p(smo_n+1) >limit_c
alpha_p(smo_n+1) = limit_c;
end
alpha_p(smo_n) = -ylabel(smo_n)*(ylabel(smo_n+1)*alpha_p(smo_n+1)+alpha_p_temp‘*ylabel_temp);
end
end
标签:
原文地址:http://www.cnblogs.com/LaoAnchor/p/4531741.html