标签:
题意:求从区间[L, R]内有多少个数是平衡数,平衡数是指以10进制的某一位为中心轴,左右两边的每一位到中心轴的距离乘上数位上的值的和相等。0<=L<=R<=1e18
思路:由于任何非0正数最多只有1个位置作为中心轴使得它是平衡数。于是可以按中心轴的位置分类统计答案。令dp[p][i][j]表示中心轴在p位(p>=0)前i位且左边比右边的加权和已经多j的方案数,枚举当前第i位放的数k,那么dp[p][i][j]=∑dp[p][i-1][j+(p-i+1)*k]。
求出dp值后,只需从高位向低位统计,统计时也是按中心轴分类,即枚举中心轴,然后根据前多少位相同,维护一下已确定的数到中心轴的加权和,然后加上对应dp值。由于0这个数无论以什么作为中心轴都会使答案加1,所以最后需减去重复的。

1 #pragma comment(linker, "/STACK:10240000,10240000") 2 3 #include <iostream> 4 #include <cstdio> 5 #include <algorithm> 6 #include <cstdlib> 7 #include <cstring> 8 #include <map> 9 #include <queue> 10 #include <deque> 11 #include <cmath> 12 #include <vector> 13 #include <ctime> 14 #include <cctype> 15 #include <set> 16 #include <bitset> 17 #include <functional> 18 #include <numeric> 19 #include <stdexcept> 20 #include <utility> 21 22 using namespace std; 23 24 #define mem0(a) memset(a, 0, sizeof(a)) 25 #define mem_1(a) memset(a, -1, sizeof(a)) 26 #define lson l, m, rt << 1 27 #define rson m + 1, r, rt << 1 | 1 28 #define rep_up0(a, b) for (int a = 0; a < (b); a++) 29 #define rep_up1(a, b) for (int a = 1; a <= (b); a++) 30 #define rep_down0(a, b) for (int a = b - 1; a >= 0; a--) 31 #define rep_down1(a, b) for (int a = b; a > 0; a--) 32 #define all(a) (a).begin(), (a).end() 33 #define lowbit(x) ((x) & (-(x))) 34 #define constructInt4(name, a, b, c, d) name(int a = 0, int b = 0, int c = 0, int d = 0): a(a), b(b), c(c), d(d) {} 35 #define constructInt3(name, a, b, c) name(int a = 0, int b = 0, int c = 0): a(a), b(b), c(c) {} 36 #define constructInt2(name, a, b) name(int a = 0, int b = 0): a(a), b(b) {} 37 #define pchr(a) putchar(a) 38 #define pstr(a) printf("%s", a) 39 #define sstr(a) scanf("%s", a) 40 #define sint(a) scanf("%d", &a) 41 #define sint2(a, b) scanf("%d%d", &a, &b) 42 #define sint3(a, b, c) scanf("%d%d%d", &a, &b, &c) 43 #define pint(a) printf("%d\n", a) 44 #define test_print1(a) cout << "var1 = " << a << endl 45 #define test_print2(a, b) cout << "var1 = " << a << ", var2 = " << b << endl 46 #define test_print3(a, b, c) cout << "var1 = " << a << ", var2 = " << b << ", var3 = " << c << endl 47 #define mp(a, b) make_pair(a, b) 48 #define pb(a) push_back(a) 49 50 typedef unsigned int uint; 51 typedef long long LL; 52 typedef pair<int, int> pii; 53 typedef vector<int> vi; 54 55 const int dx[8] = {0, 0, -1, 1, 1, 1, -1, -1}; 56 const int dy[8] = {-1, 1, 0, 0, 1, -1, 1, -1 }; 57 const int maxn = 1e5 + 7; 58 const int md = 100000007; 59 const int inf = 1e9 + 7; 60 const LL inf_L = (LL)1e18 + 7; 61 const double pi = acos(-1.0); 62 const double eps = 1e-6; 63 64 template<class T>T gcd(T a, T b){return b==0?a:gcd(b,a%b);} 65 template<class T>bool max_update(T &a,const T &b){if(b>a){a = b; return true;}return false;} 66 template<class T>bool min_update(T &a,const T &b){if(b<a){a = b; return true;}return false;} 67 template<class T>T condition(bool f, T a, T b){return f?a:b;} 68 template<class T>void copy_arr(T a[], T b[], int n){rep_up0(i,n)a[i]=b[i];} 69 int make_id(int x, int y, int n) { return x * n + y; } 70 71 struct Node { 72 LL a[808]; 73 LL &operator [] (const int x) { 74 return a[x + 401]; 75 } 76 } dp[20][20]; 77 78 void div_digit(LL x, int a[], int &n) { 79 int p = 0; 80 a[p ++] = x % 10; 81 x /= 10; 82 while (x) { 83 a[p ++] = x % 10; 84 x /= 10; 85 } 86 n = p; 87 } 88 89 void init() { 90 rep_up0(p, 18) dp[p][0][0] = 1; 91 rep_up0(p, 18) { 92 rep_up1(i, 17) { 93 for (int j = -400; j <= 400; j ++) { 94 rep_up0(k, 10) { 95 int val = j + (p - i + 1) * k; 96 if (val < -400 || val > 400) continue; 97 dp[p][i][j] += dp[p][i - 1][val]; 98 } 99 } 100 } 101 } 102 } 103 104 LL calc(LL n) { 105 if (n == -1) return 0; 106 if (n == (LL)1e18) return (LL)12644920956811384; 107 LL ans = 0; 108 int a[20], len; 109 div_digit(n, a, len); 110 rep_up0(p, 18) { 111 int sum = 0; 112 rep_down0(i, len) { 113 rep_up0(j, a[i]) { 114 int val = sum + (p - i) * j; 115 if (val < -400 || val > 400) continue; 116 ans += dp[p][i][val]; 117 } 118 sum += a[i] * (p - i); 119 } 120 } 121 rep_up0(p, 18) { 122 int sum = 0; 123 rep_down0(i, len) { 124 sum += a[i] * (p - i); 125 } 126 if (sum == 0) ans ++; 127 } 128 return ans - 17; 129 } 130 131 int main() { 132 //freopen("in.txt", "r", stdin); 133 init(); 134 int T; 135 cin >> T; 136 LL n, m; 137 while (T --) { 138 cin >> n >> m; 139 cout << calc(m) - calc(n - 1) << endl; 140 } 141 return 0; 142 }
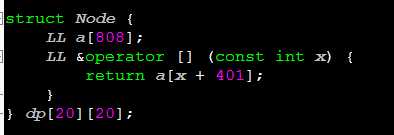
另外,灵机一动想出来一种写法(如有雷同,纯属巧合),用起来也还不错哦!
标签:
原文地址:http://www.cnblogs.com/jklongint/p/4532093.html