标签:
题解:整个数组是非降序的,所有相等元素都会聚集在一起。开一个num数组,用num[i]来记录第i段相等的元素有多少个(也就是说相当于RMQ中的元素值了),num数组的长度就是原数列不同元素的个数(段数),l数组记录i段元素的上界,r数组记录i段元素的下界,用一个mark数组记录i位置的元素属于第几段。假设询问区间为a,b:
L=mark[a],R=mark[b];
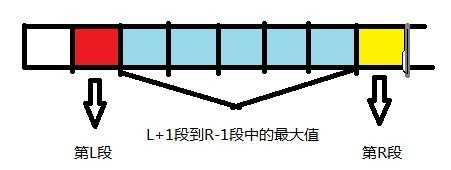
ans=max(r[L]-a+1,b-l[R]+1,夹在这两个段中最大值)
图解:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#include<queue>
#include<vector>
#include<stack>
using namespace std;
int n,q,num[100010],mark[100010],l[100010],r[100010],pos,maxnum[100010][26];
void RMQ()
{
for(int i=1;i<=pos;i++)
maxnum[i][0]=num[i];
for(int j=1;j<25;j++)
{
for(int i=1;i<n;i++)
if(i+(1<<j)-1<=n)
maxnum[i][j]=max(maxnum[i][j-1],maxnum[i+(1<<(j-1))][j-1]);
}
}
int main()
{
while(scanf("%d",&n)!=EOF)
{
if(n==0)
break;
int x,val;
scanf("%d",&q);
pos=0;
for(int i=1;i<=n;i++)
{
scanf("%d",&x);
if(x==val)
{
num[pos]++;
mark[i]=pos;
}
else
{
r[pos]=i-1;
pos++;
num[pos]=1;
val=x;
mark[i]=pos;
l[pos]=i;
}
}
r[pos]=n;
RMQ();
while(q--)
{
int x,y,ans=0;
scanf("%d%d",&x,&y);
if(mark[x]==mark[y])
{
printf("%d\n",y-x+1);
continue;
}
if(mark[x]+1<=mark[y]-1)
{
int k=(int)(log(mark[y]-mark[x]-1)/log(2.0));
ans=max(maxnum[mark[x]+1][k],maxnum[mark[y]-(1<<k)][k]);
}
ans=max(ans,max(r[mark[x]]-x+1,y-l[mark[y]]+1));
printf("%d\n",ans);
}
}
return 0;
}
标签:
原文地址:http://www.cnblogs.com/water-full/p/4533227.html