标签:
Description
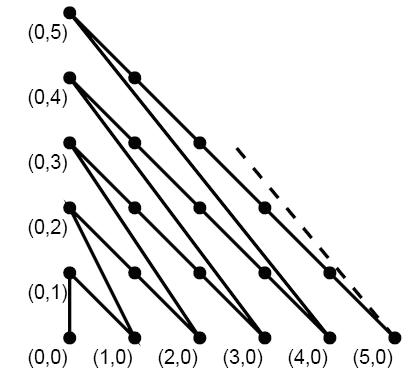
Input
Output
Sample Input
5 0 0 0 1 0 0 1 0 2 3 3 1 99 99 9 9 5 5 5 5
Sample Output
1.000 2.414 10.646 54985.047 0.000
思路:a了这道题,感觉还不错~中午写出来了,但是开始交的时候错了,第二次交时候数组越界了。好像提交只需要写一组N就行。(0,0)(0,1)(1,0)(0,2)(1,1)(2,0)(0,3)(1,2)(2,1)(3,0)//横纵坐标和是数组下标i 横坐标逐渐递增加一,纵坐标减一(0,4)(1,3)(2,2)(3,1)(4,0)(0,5)(1,4)(2,3)(3,2)(4,1)(5,0)…… 同一行之间距离是根号2,#include<iostream> #include<stdio.h> #include<math.h> using namespace std; struct Point { int x; int y; }; Point point[500][500]; void diabiao() { int i,j,xkai,ykai; for(i=0;i<=300;i++) { xkai=0; ykai=i; for(j=0;j<=i;j++) { point[i][j].x=xkai; point[i][j].y=ykai; xkai++; ykai--; } } } double distance(int x1,int y1,int x2,int y2) { return sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1)); } int main() { int N,i,x1,y1,x2,y2; diabiao(); cin>>N; while(N--) { int flag1=0; int flag2=0; int pos1,pos2; double sum=0; cin>>x1>>y1>>x2>>y2; if(x1+y1==x2+y2) { for(i=0;i<=x1+y1;i++) { if(point[x1+y1][i].x==x1 && point[x1+y1][i].y==y1) { flag1=1; pos1=i; } if(point[x1+y1][i].x==x2 && point[x1+y1][i].y==y2) { flag2=1;pos2=i; } if(flag1==1 &&flag2==1) break; } printf("%.3lf\n",abs(pos1-pos2)*sqrt(2)); } else { if(x1+y1>x2+y2) { int t; t=x1; x1=x2; x2=t; t=y1; y1=y2; y2=t; } for(i=0;i<=x1+y1;i++) { if(point[x1+y1][i].x==x1 && point[x1+y1][i].y==y1) { pos1=i; break; } } sum+=(x1+y1-pos1)*sqrt(2); for(i=0;i<=x2+y2;i++) { if(point[x2+y2][i].x==x2 && point[x2+y2][i].y==y2) { pos2=i; break; } } sum+=pos2*sqrt(2); //(x1+y1,0) (0,x2+y2) int s=x1+y1; while(1) { if(x2+y2-(s)==1) { sum+=distance(s,0,0,s+1); printf("%.3lf\n",sum); break; } else { sum+=distance(s,0,0,s+1); sum+=sqrt(2)*(s+1); s=(s+1); } } } } return 0; }
标签:
原文地址:http://blog.csdn.net/zuguodexiaoguoabc/article/details/46046687