云端大数据实战记录-大数据推荐

时间：2014-06-16 14:21:39 阅读：351 评论：0 收藏：0 [点我收藏+]

标签：大数据分布式计算云计算机器学习

(转载请注明出处：http://blog.csdn.net/buptgshengod)

1.背景

这是博主第一次大数据实战的经历，之前都是自己写一些算法然后测试很小的数量级。这次是真正接触到TB集的数据，而且完全是在云端处理。下面就把这次的经历简单分享一下。

首先简单介绍一下这次比赛的环境吧：

1.云：采用的是阿里云

2.数据：从四月十五号到八月十五号期间，用户两千多万的购买行为（包括时间，购买、收藏、购物车的次数）

3.工具：阿里提供的xlab（里面有很多算法，随机森林、逻辑回归、knn等）、odps（也就是sql数据库）、mapreduce环境（java分布式计算）、udf（主要是提供sql的一些function功能）。

4.目的：预测八月十五号之后的用户行为。

2.工具的简单说明

（1）odps

这个主要是sql数据库的一些简单操作。sql玩的溜的大神们都可以用sql语句实现很多的算法，当然博主只能用sql合并表、简单查询之类的。比如我们实现一个简单的查询去重的功能，odps可以通过分布式计算将任务量分不给很多云端服务器，然后快速的执行大数据的查询工作。差不多三百多万的数据查询只用一分钟就解决的，如果要是离线测试，估计得几十分钟，这就是云的魅力。

select distinct * from table_name;

（2）mapreduce

mapreduce简称mr，主要是实现一些复杂的逻辑的时候使用，比如说像是一些算法。我们使用mr实现算法，可以通过配置文件设置一些分布式的规则，然后将jar文件post到云端就实现了云计算。上一张mr的图片。

3.TRY

因为这次比赛的奖金很高，阿里组织的也很靠谱，所以参赛的队伍实力都很强的。看眼排行榜就知道了。博主码农大学(北邮)还在两百多名徘徊 bubuko.com,布布扣

（1）第一次尝试-尿布与啤酒的幻想破灭

做推荐系统的应该都知道尿布与啤酒的故事。这是一个协同过滤的问题，很多大的电商网站都是通过icf也就是关于商品的协同过滤来进行推荐的。博主最早也是通过聚类算法，找出了一些志趣相投的人（买相同品牌的商品的人），具体的实现是通过xlab里的聚类算发还有udf实现的。结果是准确率不到百分之一，不知道是我的方法不对还是本来这种数据集不适合用cf。

（2）利用规则

因为博主是金牌买家，所以将心比心，我们可以轻易的得出几个规则可能准确率比较高。

规则一：用户每个月都会购买的商品

规则二：用户最后一个月点击n次的商品

规则三：用户购买次数超过k的商品

利用这些规则推荐，虽然也能取得一个相对不错的结果，但是想更进一步就要通过算法了。

（3）算法：随机森林

什么是随机森林，就是用很对决策树来实现的数据集的分类预测，具体的算法如下。

算法的主要思想就是将数据集按照特征对目标指数的影响由高到低排列。行成一个二叉树序列，进行分类。现在的问题关键就是，当我们有很多特征值时，哪些特征值作为父类写在二叉树的上面的节点，哪下写在下面。我们可以直观的看出上面的特征值节点应该是对目标指数影响较大的一些特征值。那么如何来比较哪些特征值对目标指数影响较大呢。这里引出一个概念，就是信息熵。

信息理论的鼻祖之一Claude E. Shannon把信息（熵）定义为离散随机事件的出现概率。说白了就是信息熵的值越大就表明这个信息集越混乱。

信息熵的计算公式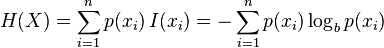， $bubuko.com,布布扣$ （建议去wiki学习一下）

这里我们通过计算目标指数的熵和特征值得熵的差，也就是熵的增益来确定哪些特征值对于目标指数的影响最大。

第一部分-计算熵：函数主要是找出有几种目标指数，根据他们出现的频率计算其信息熵。

[python]view plaincopy
def calcShannonEnt(dataSet):  
    numEntries=len(dataSet)  
      
    labelCounts={}  
  
    for featVec in dataSet:  
        currentLabel=featVec[-1]  
         
        if currentLabel not in labelCounts.keys():  
            labelCounts[currentLabel]=0          
        labelCounts[currentLabel]+=1  
    shannonEnt=0.0  
      
    for key in labelCounts:  
           
         prob =float(labelCounts[key])/numEntries          
         shannonEnt-=prob*math.log(prob,2)  
  
    return shannonEnt           

第二部分-分割数据因为要每个特征值都计算相应的信息熵，所以要对数据集分割，将所计算的特征值单独拿出来。

[python]view plaincopy
def splitDataSet(dataSet, axis, value):  
    retDataSet = []  
    for featVec in dataSet:  
        if featVec[axis] == value:  
            reducedFeatVec = featVec[:axis]     #chop out axis used for splitting              
            reducedFeatVec.extend(featVec[axis+1:])        
            retDataSet.append(reducedFeatVec)            
    return retDataSet  

第三部分-找出信息熵增益最大的特征值

[python]view plaincopy
def chooseBestFeatureToSplit(dataSet):  
    numFeatures = len(dataSet[0]) - 1      #the last column is used for the labels  
    baseEntropy = calcShannonEnt(dataSet)  
    bestInfoGain = 0.0; bestFeature = -1  
    for i in range(numFeatures):        #iterate over all the features  
        featList = [example[i] for example in dataSet]#create a list of all the examples of this feature  
         
        uniqueVals = set(featList)       #get a set of unique values  
          
        newEntropy = 0.0  
        for value in uniqueVals:  
            subDataSet = splitDataSet(dataSet, i, value)  
            prob = len(subDataSet)/float(len(dataSet))  
            newEntropy += prob * calcShannonEnt(subDataSet)       
        infoGain = baseEntropy - newEntropy     #calculate the info gain; ie reduction in entropy  
          
        if (infoGain > bestInfoGain):       #compare this to the best gain so far  
            bestInfoGain = infoGain         #if better than current best, set to best  
            bestFeature = i  
    return bestFeature                      #returns an integer  

第四部分-建立决策树

[python]view plaincopy
def createTree(dataSet,labels):  
    #把所有目标指数放在这个list里  
    classList = [example[-1] for example in dataSet]  
    #下面两个if是递归停止条件，分别是list中都是相同的指标或者指标就剩一个。  
    if classList.count(classList[0]) == len(classList):   
        return classList[0]  
    if len(dataSet[0]) == 1:   
        return majorityCnt(classList)  
    #获得信息熵增益最大的特征值  
    bestFeat = chooseBestFeatureToSplit(dataSet)  
    bestFeatLabel = labels[bestFeat]     
    #将决策树存在字典中  
    myTree = {bestFeatLabel:{}}  
    #labels删除当前使用完的特征值的label  
    del(labels[bestFeat])  
    featValues = [example[bestFeat] for example in dataSet]  
    uniqueVals = set(featValues)  
    #递归输出决策树  
    for value in uniqueVals:         
        subLabels = labels[:]       #copy all of labels, so trees don‘t mess up existing labels  
         
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)  
    return myTree  

4.具体实现

以上是用python写的决策树算法，在比赛中xlab工具已经提供这些底层的算法，主要的工作是要特征值选择和调试参数。

除了数据集提供的基本的几个参数以外，主要是通过一些特征间的组合又找出了十个左右的特征。

（1）特征提取

我的经验是在特征组合的时候，如果某个值的区间特别大，我们可以使用log函数来处理。比如说data的数值是1-100，而click的数值是0-3。如果这个时候我们直接提取特征data_click=click/data的话，可能会造成曲线波动比较大。这个时候可以用log函数，data_click=ln(1+data)来提取特征，会使曲线变得更加平滑。

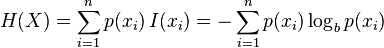特征值得平方是个不错的选择。因为y=x+1是一条直线。而如果是 bubuko.com,布布扣

，就会变为一条曲线，更容易实现拟合。