标签:
第1章 开篇
问题:
输入:
一个最多包含n个正整数的文件,每个数都小于n,其中n=107。如果在输入文件中有任何整数重复出现就是致命错误。没有其它数据与该整数相关联。
输出:
按升序排列的输入整数的列表。
约束:
最多有(大约)1MB的内存空间可用,有充足的磁盘存储空间可用。运行时间最多几分钟,运行时间10秒就不需要进一步优化了。
解决方案:
位向量
//phase 1:initialize set to empty for i = [0,n) bit[i] = 0 //phase 2: insert present elements into the set for each i in the input file bit[i] = 1 //phase 3: write sorted output for i = [0,n) if bit[i] == 1 write i on the output file
设置、清除以及测试位值
#define BITSPERWORD 32#define SHIFT 5#define MASK 0x1F#define N 10000000int a[1+N/BITSPERWORD];void set(int i){ a[i>>SHIFT] |= (1<<(i & MASK));}void clr(int i){ a[i>>SHIFT] &= ~(1<<(i & MASK));}int test(int i){ return a[i>>SHIFT] & (1<<(i & MASK));}
第2章 啊哈!算法
2.1 三个问题
A.给定一个最多包含40亿个随机排列的32位整数的顺序文件,找出一个不在文件中的32位整数(在文件中至少缺失一个这样的数--为什么?)在具有足够内存的情况下,如何解决该问题?如果有几个外部的“临时”文件可用,但是仅有几百字节的内存,又该如何解决该问题?
B.将一个n元一维向量向左旋转i个位置。例如,当n=8且i=3时,向量abcdefgh旋转为defghabc。
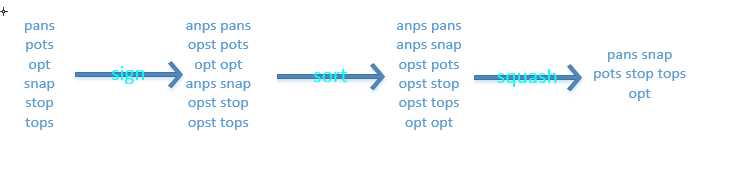
C.给定一个英语字典,找出其中的所有变位词集合,例如,"pots","stop","tops"互为变位词,因为每个单词可以通过改变其它单词中字母的顺序得到。
A:
227=1,3421,7728
232=42,9496,7296
根据二进制位从高位开始分堆,缺失整数出现在较少的堆里。
B:
左右手翻手。
C:
将单词内字母排序使得同一个变位词类中的单词具有标准型。通过给每条记录添加一个额外的关键字,并按照这些关键字进行排序。
第3章 数据决定程序结构
3.2 格式信函编程
Welcome back, Jane!
We hope taht you and all the members
of the Public family are constantly
reminding your neighbors there
on Maple Street to shop with us.
As usual, we will ship your order to
Ms. Jane Q. public
600 Maple Street
Your Town,Iowa 12345
..
其在数据库中查询到以下数据
Public|Jane|Q|Ms.|600|Maple Street|Your Town|Iowa|12345
一个巧妙的办法是编写一个格式信函发生器(form letter gennerator)。该发生器基于下面所示的格式信函模板(form letter schema)。将格式与数据分离。
Welcome back, $1!
We hope taht you and all the members
of the $0 family are constantly
reminding your neighbors there
on $5 to shop with us.
As usual, we will ship your order to
$3 $1 $2. $0
$4 $5
$6, $7 $8
..
3.3 一组示例
出错信息:
混乱系统的数百个出错信息散布在所有代码中。而清晰的系统则通过一个专用的函数来访问这些出错信息。
日期函数:
单词分析:
3.5 用于特殊数据的强大工具
超文本:
名字-值对:
电子表格:
数据库:
第4章 编写正确的程序
习题6
David Gries在其Science of Programming中将下面的问题称为“咖啡罐问题”。给定一个盛有一些黑色豆子和一些白色豆子的咖啡罐以及一大堆“额外”的黑色豆子,重复以下过程,直至罐中仅剩一颗豆子为止。
从罐中随机选取两颗豆子,如果颜色相同,就将它们都扔掉并且放入一个额外的黑色豆子;如果颜色不同,就将白色的豆子放回罐子中,而将黑色的豆子扔掉。
证明该过程会终止。最后留在罐中的豆子颜色与最初罐中白色豆子和黑色豆子的数量有何函数关系?
每次操作都用两颗豆子换一颗,所以这个过程是一定会终止的。
白豆的个数的奇偶性保持不变。因此,当且仅当罐中最初的白豆个数为奇数时,最后留下的豆子才可能是白色的。
第6章 程序性能分析
从几个不同的层面来改进:
算法和数据结构
算法调优
数据结构重组
代码调优
硬件
第7章 粗略估算
7.4 Little定律
考虑一个带有输入和输出的任意系统,Little定律指出“系统中物体的平均数量等于物体离开系统的平均速率和每个物体在系统中停留的平均时间的乘积”(并且如果物体离开和进入系统的总体出入流是平衡的,那么离开速率也就是进入速率。)
第8章 算法设计技术
问题:
输入:具有n个浮点数的向量x。
输出:输入向量的任何连续子向量中的最大和。
分治算法
float maxsum3(l,u) if (l > u) return 0 if (l == u) return max(0,x[l]) m = (l + u) /2-
- /*find max crossing to left*/
lmax = sum = 0 for ( i = m; i >= l; i--) sum += x[i] lmax = max(sum ,lmax)- /*find max crossing to right*/
rmax = sum = 0 for i = (m, u] sum += x[i] rmax = max(rmax,sum) return max(lmax+rmax, maxsum3(l,m),maxsum3(m+1,u))
时间复杂度:O(nlogn)。一种非正式的论证是,该算法在每层递归中都执行O(n)次操作,而计有O(logn)层递归。
扫描算法
maxsofar = 0 maxendinghere = 0 for i = [0,n) /*invariant:maxendinghere and maxsofar are accurate for x[0...i-1]*/ maxendinghere = max(maxendinghere + x[i], 0) maxsofar = max(maxsofar, maxendinghere)
时间复杂度:O(n),因此我们称之为线性算法
习题14
给定整数m、n和实数向量x[n],请找出使总和x[i]+...+x[i+m]最接近0的整数i(0<=i<n-m)。
初始化累加数组cum,使得cum[i] = x[0] + ... + x[i],如果cum[l-1] = cum[u],那么子向量x[l..u]之和就为0。
第9章 代码调优
大手术--二分搜索
i = 512l = -1if x[511] < t l = 1000 - 512while i != 1 /* invariant: x[l] < t && x[l+i] >= t && i = 2^j */ nexti = i / 2 if x[l+nexti] < t l = l + nexti i = nexti else i = nexti/*assert i == 1 && x[l] < t && x[l+i] >= t*/p = l+1if p > 1000 || x[p] != t p = -1
习题12
人们在调优程序时有时会从数学的角度考虑而不是从代码的角度考虑。为了计算下面的多项式:
y = anxn + an-1xn-1 +...+ a1x1 + a0
如下的代码使用了2n次乘法。请给出一个更快的函数。
y = a[0]
xi = 1
for i = [1,n]
xi = x*xi
y = y + a[i]*xi
_________________________________________
y = a[n]
for ( i = n-1;i>=0;i--)
y = x*y + a[i]
第10章 节省空间
节省空间的同时,我们通常会在运行时间上得到想要的副作用:程序变小后加载更快,也更容易填入高速缓存中;此外,需要操作的数据变少通常也意味着操作时间减少。
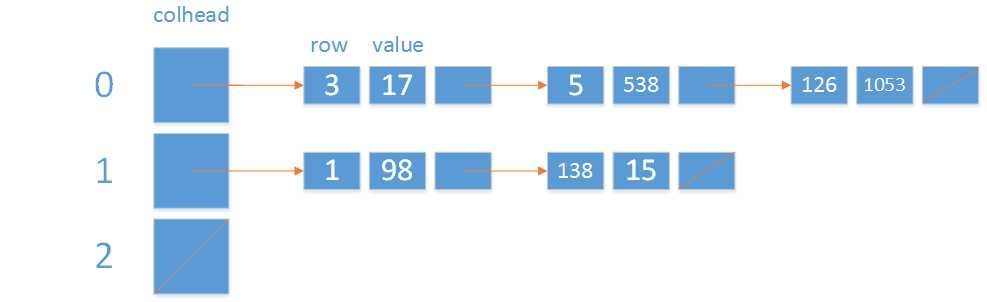
稀疏矩阵的一种浅显的表示法就是用数组表示所有的列,同时使用链表来表示给定列中的活跃元素。
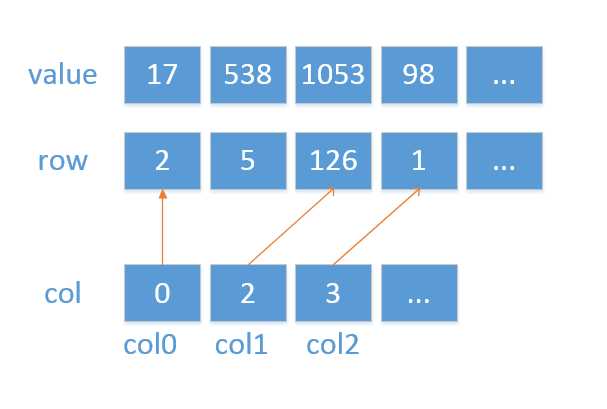
转化为平行数组:
说明:col0,及col1之间所指的范围是col0上所有的行号。例如这里列0上在第2,5排上有数据,而且分别是17,538。
注:其实本质上可以理解为存储一对(row,col),或者(row,col,value),在C++中可以用map来做。在PYTHON中可用元组。
稀疏数据结构
数据压缩
分配策略
主要是动态分配
垃圾回收
代码空间技术
函数定义
解释程序
其实就是脚本
翻译成机器语言
第11章 排序
插入排序
for i = [1,n) t = x[i] for ( j = i; j> 0 && x[j-1] > t; j--) x[j] = x[j-1] x[j] = t
快速排序
void qsort1(l,u) if (l >= u) return m = l for i = [l+1,u] /* invariant: x[l+1..m] < x[l] && x[m+1..i-1] >= x[l]*/ if (x[i] < x[l]) swap(++m,i) swap(l,m) /*x[l..m-1] < x[m] <= x[m+1..u] */ qsort1(l,m-1) qsort1(m+1,u)
分析:
考虑一种极端的情况:n个相同元素组成的数组。
对于这种输入,插入排序的性能非常好:每个元素需要移动的距离都为0,所以总的时间为O(n),
但qsort1函数的性能非常糟糕,n-1次划分中每次划分都需要0(n)时间来去掉一个元素,所以总的时间为O(n2)。注:这是因为划分出来的分区都是n个元素,最好的分区方式是一半元素为一个分区,这样能得到nlogn的复杂度。可以采取随机主元的方式来得到更好的性能。
swap(1,randint(l,u));
void qsort3(l,u) if l >= u return t = x[l]; i = l; j = u+1; loop do i++ while i <= u && x[i] < t do j-- while x[j] > t if ( i > j) break swap(i,j) swap(l,j) qsort3(l,j-1) qsort3(j+1,u)
快速排序程序花费了大量的时间来排序很小的子数组。如果用插入排序之类的简单方法来排序这些很小的子数组,程序的速度会更快。
在很小的子数组上调用快速排序时(l和u非常接近),不执行任何操作。程序结束时,数组不是有序的,而是被组合成一块一块的,块与块间有序,即在左边的块中所有元素都比右边的块中所有元素都小。
void qsort4(l,u) if u - l < cutoff return swap(l,randint(l,u)) t = x[l]; i = l; j = u+1 loop do i++; while i <=u && x[i] < t do j--; while x[j] > t if i > j break; temp = x[i]; x[i] = x[j]; x[j] = temp swap(l,j) qsort4(l,j-1) qsort4(j+1,u)
习题9
编写程序,在O(n)时间内从数组x[0..n-1]中找出第k个最小的元素。算法可以对x中的元素进行排序。
void select1(l,u,k)
pre l <= k <= u
post x[l..k-1] <= x[k] <= x[k+1..u]
if l >= u
return
swap(l, randint(l,u))
t = x[l], i = 1; j = u + 1
loop
do i++; while i <= u && x[i] < t
do j--; while x[j] > t
if i > j
break
temp = x[i]; x[i] = x[j]; x[j] = temp
swap(l,j)
if j < k
select1(j+1,u,k)
else if j > k
select1(l,j-1,k)
习题11
编写一个“宽支点”划分函数,使得结果如下图所示:
如何将这个函数应用到快速排序中?
第12章 取样问题
问题:
程序的输入包含两个整数m和n,其中m<n。输出是0~n-1范围内m个随机整数的有序列表,不允许重复。从概率的角度来说,我们希望得到没有重复的有序选择,其中每个选择出现的概率相等。
一般来说,如果要从r个剩余的整数中选出s个,我们以概率s/r选择下一个数。
void genknuth(int m, int n){ for ( int i = 0; i < n; i++) /*select m of remainning n-i*/ if ((bigrand() % (n-i)) < m) { cout << i << "\n"; m--; }}
分析:
((bigrand() % (n-i)) < m
可以理解为:
[m / (bigrand() % (n-i)] > 1
其它解决方案:
一种解决方案是在一个初始为空的集合里面插入随机整数,直到个数足够。
void gensets(int m, int n){ std::set<int> s; while (s.size() < m) s.insert(bigrand() % n); std::set<int>::iterator i; for ( i = s.begin(); i != s.end(); i++) std::cout << *i << std::endl;}
另一种方法是把包含整数0~n-1的数组顺序打乱,然后把前m个元素排序输出。
for i = [0,n) swap(i, randint(i,n-1))
如何从n个对象(可以依次看到这n个对象,但事先不知道n的值)中随机选择一个?具体说来,如何在事先不知道文本文件行数的情况下读取该文件,从中随机选择并输出一行?
我们总选择第1行,并以概率1/2选择第2行,以概率选择第3行,依此类推。在这一过程结束时,每一行选中的概率是相等的(1/n,其中n是文件的总行数)
i = 0
while more input lines
with probability 1.0/++i
choice = this input line
print choice
第14章 堆
堆解决两个重要的问题:
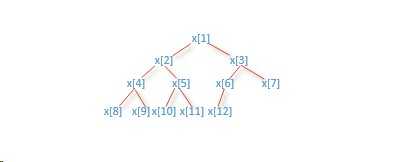
注意:堆使用的是从下标1开始的数组。
树中常见的函数定义如下:
root = 1
value(i) = x[i]
leftchild(i) = 2*i
rightchild(i) = 2*i + 1
parent(i) = i / 2
null(i) = ( i < 1 ) or ( i > n)
void siftup(n) pre n > 0 && heap(1,n-1) post heap(1,n) i = n loop /* invariant: heap(1,n) except perhaps between i and left parent*/ if 1 == i break; p = i / 2 if x[p] <= x[i] break swap(p,i) i = p
void siftdown(n) pre heap(2,n) && n >= 0 post heap(1,n) i = 1 loop /* invariant: heap(1,n) except perhaps between i and its (0,1 or 2) children*/ c = 2*i if c > n break /* c is the left child of i*/ if c+1 <= n /* c+1 is the right child of i*/ if x[c+1] < x[c] c++ /* c is the lesser child of i*/ if x[i] <= x[c] break swap(c,i) i = c
优先级队列
void insert(t) if n >= maxsize /* report error*/ n++ x[n] = t /* heap(1,n-1)*/ siftup(n) /*heap(1,n)*/
int extractmin() if n < 1 /* report error*/ t = x[1] x[1] = x[n--] /*heap(2,n)*/ siftdown(n) /*heap(1,n)*/ return t
排序算法
优先队列提供了一种简单的向量排序算法:首先在优先级队列中依次插入每个元素,然后按序删除它们。
template<class T>void pqsort(T v[],int n){ priqueue<T> pq(n); int i; for (i = 0; i < n; i++) pq.insert(v[i]); for (i = 0; i < n; i++) v[i] = pq.extractmin();}
堆排序:
第一阶段,建立堆。
下面这段代码通过将元素在数组中向上筛选来建立heap(1,n):
for i = [2,n] /*invariant: heap(1,i-1)*/ siftup(i) /*heap(1,i)
第二阶段,使用堆来建立有序序列。
for ( i = n; i >= 2; i--) /* heap(1,i) && sorted(i+1,n) && x[1..i] <= x[i+1..n]*/ swap(1,i) /* heap(2,i-1) && sorted(i,n) && x[1..i-1] <= x[i..n]*/ siftdown(i-1) /* heap(1,i-1) && sorted(i,n) && x[1..i-1] <= x[i..n]*/
完整的堆排序只要5行代码
for i = [2,n] siftup(i)for ( i = n; i >= 2; i--) swap(1,i) siftdown(i-1)
习题4
如何使用优先级队列的堆实现解决下列问题?当输入有序时,你的答案有什么变化?
a.构建赫夫曼码(绝大多数关于信息理论的书和许多关于数据结构的书都会讨论这种编码)
b.计算大型浮点数集合的和。
c.在存有10亿个数的文件中找出最大的100万个数。
d.将多个较小的有序文件归并为一个较大的有序文件(在实现1.3节那样的基于磁盘的归并排序程序时会出现这种问题)。
习题7
在一些计算机上,除以2以求出当前范围的中点是二分搜索程序中开销最大的部分。假设我们已经正确构建了待搜索的数组,说明如何使用乘以2的操作来替代除法。给出建立并搜索这样一个数组的算法。
修改后的二分搜索从i=1开始,每次迭代将i设置为2i或2i+1。元素x[1]包含中值,x[2]包含第一个四分值,x[3]包含第三个四分位值,等等。
考虑把一个【2k-1元】的有序数组a拷贝到一个“堆搜索”数组b中:a中的奇数位的元素按顺序放到b的后半部分,模4余2位置的元素按顺序放到b中剩余部分的后半部分,等等。
习题9
证明在优先级队列的堆实现中,insert和extractmin的对数运行时间都在一个最佳常数因子范围内。
第15章 字符串
后缀数组:
while (ch = getchar()) != EOF a[n] = &c[n] c[n++] = chc[n] = 0
说明:元素a[0]指向整个字符串,下一个元素指向第二个字符开始的数组后缀,等等。对于输入字符串“banana”,该数组能够表示下面这些后缀:
a[0]:banana
a[1]:anana
a[2]:nana
a[3]:ana
a[4]:na
a[5]:a
如果某个长字符串在数组c中出现两次,那么它将出现在两个不同的后缀中,因此我们对数组排序以寻找相同的后缀。“banana”数组排序为:
a[0]:a
a[1]:ana
a[2]:anana
a[3]:banana
a[4]:na
a[5]:nana
然后我们就可以扫描数组,通过比较相邻元素来找出最长的重复字符串,本例为“ana”。
多数事件发生在上下文中。假定我们要随机生成一年的华氏温度数据,0~100范围内的365个随机整数序列无法欺骗一般的观察者。我们可以通过把今天的温度设置为昨天温度的(随机)函数来得到更可信的结果;如果今天是850C,那么明天不太可能是150C。
香农1948年的著名论文《Mathematical Theory of Communication》:“以构建【字母级别的1阶文本】为例,我们随机打开一本书并在该页随机选择一个字母记录下来。然后翻到另一页开始读,直到遇到该字母,此时记录其后面的那个字母。再翻到另外一页搜索上述第二个字母并记录下其后面的那个字母,依此类推。对于【字母级别的1阶、2阶文本和单词级别的0阶、1阶文本】,处理过程是类似的。”
我们生成K阶马尔可夫链的C程序最多在数组inputchars中存储5MB的文本:
int k = 2;char inputchars[5000000];cahr *word[1000000];int nword = 0;
说明:数组word作为一种指向字符的后缀数组,变量nword保存单词的数量。
我们用下面的代码读取文件:
word[0] = inputcharswhile scanf("%s",word[nword]) != EOF word[nword+1] = word[nword] + strlen(word[nword]) + 1 nword++
读完输入后,我们将对word数组进行排序,以得到指向同一个K单词序列的所有指针。下列函数完成比较工作:
int wordncmp(char *p, char *q) n = k for ( ; *p == *q; p++, q++) if (*p == 0 && --n == 0) return 0 return *p - *q
说明:比较p和q的前k个单词。如果前K个单词相同返回0,不同时,返回差别。
phrase = inputcharsfor ( wordsleft = 10000; wordsleft > 0; wordsleft--) l = -1 u = nword
while l+1 != u m = (l+u)/2 if wordncmp(word[m],phrase) < 0 l = m else u = m
for ( i = 0; wordncmp(phrase,word[u+i]) == 0; i++) if rand() % (i+1) == 0 p = word[u+i]
phrase = skip(p,1) if strlen(skip(phrase,k-1)) == 0 break print skip(phrase,k-1)
说明:使用二分搜索来定位phrase的第一次出现,并在所有相同的phrase中随机选择一个。如果所选择的phrase中第K个单词的长度为0,那么当前短语是文档中的最后一个,因此我们跳出循环。
习题9
给定两个输入文本,找出它们共有的最长字符串。
习题16
如何使用本章的方法形成字典的单词列表?如何在不使用字典的前提下建立拼写检查器?如何在不使用语法规则的前提下建立语法检查器?
习题17
研究一下在语音识别和数据压缩等应用中,与k连字母分析有关的方法是如何使用的。
附录D 代码调优法则
D.1 空间换时间法则
修改数据结构。为了减少数据上的常见运算所需要的时间,我们通常可以在数据结构中增加额外的信息,或者修改数据结构中的信息使之更易访问。
存储预先计算好的结果。对于开销较大的函数,可以只计算一次,然后将计算结果存储起来以减少开销。以后需要该函数时,可以直接查表而不需要重新计算。
高速缓存。最经常访问的数据,其访问开销应该是最小的。
懒惰求值。除非需要,否则不对任何一项求值。这一策略可以避免对不必要的项求值。
D.2 时间换空间法则
堆积。密集的存储可以通过增加存储和检索数据所需的时间来减少存储开销。
解释程序。使用解释程序通常可以减少表示程序所需要的空间,在解释程序中常见的操作序列以一种紧凑的方式表示。
D.3 循环法则
将代码移出循环。与其在循环的每次迭代时都执行一次某种计算,不如将其移到循环体外,只计算一次。
合并计算条件。高效的内循环应该包含尽量少的测试条件,最好只有一个。因此,程序员应尽量用一些退出条件来模拟循环的其它退出条件。
哨兵是该法则的常见应用:在数据结构的边界上放一个哨兵以减少测试是否已循环结束的开销。
展开循环。展开循环可以减少修改循环下标的开销,对于避免管道延迟、减少分支以及增加指令级的并行性也都很有帮助。
删除赋值。如果内循环中很多开销来自普通的赋值,通常可以通过重复代码并修改变量的使用来删除这些赋值。具体说来,删除赋值i =j后,后续的代码必须将j视为i。
循环合并。如果两个相邻的循环作用在同一组元素上,那么可以合并其运算部分,仅使用一组循环控制操作。
D.4 逻辑法则
短路单调函数。如果我们想测试几个变量的单调非递减函数是否超过某个特定的阈值,那么一旦达到这个阈值就不再需要计算任何变量了。
该法则的一个成熟应用就是,一旦达到了循环的目的就退出循环。第10章第13章和第15章中的搜索循环都是一旦找到所需的元素就终止。
对测试条件重新排序。在组织逻辑测试的时候,应该将低开销的、经常成功的测试放在高开销的、很少成功的测试前面。
预先计算逻辑函数。在比较小的有限域上,可以用查表来取代逻辑函数。
D.5 过程法则
高效处理常见情况。应该使函数能正确处理所有情况,并能高效处理常见情况。
协同程序。通常,使用协同程序能够将多趟算法转换为单趟算法。
2.8 节的变位词程序使用了管道,这能通过一组协同程序来实现。
(注:其实就是分为多个小模块)
递归函数转换。递归函数的运行时间往往可以通过下面的转换来缩短。
将递归重写为迭代。
如果函数的最后一步是递归调用其自身,那么使用一个到其第一条语句的分支来替换该调用,这通常称为消除尾递归。(循环)
解决小的子问题时,使用辅助过程通常比把问题的规模变为0或1更有效。
并行性。在底层硬件条件下,我们构建的程序应该尽可能多地挖掘并行性。
D.6 表达式法则
编译时初始化。在程序执行之前,应该对尽可能多的变量初始化。
利用等价的代数表达式。如果表达式的求值开销太大,就将其替换为开销较小的等价代数表达式。
消除公共子表达式。如果两次对同一个表达式求值时,其所有变量都没有任何改动,那么我们可以用下面的方法避免第二次求值:存储第一次的计算结果并用其取代第二次求值。
成对计算。如果经常需要对两个类似的表达式一起求值,那么就应该建立一个新的过程,将它们成对求值。
《编程珠玑》
标签:
原文地址:http://www.cnblogs.com/codetravel/p/4534567.html


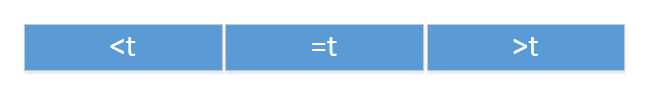


 习题10
习题10