binary tree/tree相关问题 review

时间：2015-05-28 07:04:49 阅读：120 评论：0 收藏：0 [点我收藏+]

标签：

本文主要对binary tree和tree相关问题做一个review，然后一道一道解决leetcode中的相关问题。

因为是review了，所以基本概念定义什么的就不赘述。review主要包括：inorder， postorder，preorder traversal的iterative version，（recursive比较直接，先不多解释了），level order traversal以及morris traversal。

首先定义一下binary tree，这里我们follow leetcode的定义

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
}

首先是 preorder traversal，这里使用一个stack，O(n) time， O(n) space。

 1 class Solution {
 2 public:
 3     vector<int> preorderTraversal(TreeNode *root) {
 4         vector<int> res;
 5         stack<TreeNode *> s;
 6         while(root || s.size() > 0) {
 7             if(root) {
 8                 res.push_back(root->val);
 9                 s.push(root);
10                 root = root->left;
11             }
12             else {
13                 root = s.top();
14                 s.pop();
15                 root = root->right;
16             }
17         }
18         return res;
19     }
20 };

View Code

inorder traversal，同样使用一个stack，O(n) time， O(n) space。

 1 class Solution {
 2 public:
 3     vector<int> inorderTraversal(TreeNode *root) {
 4         vector<int> res;
 5         stack<TreeNode *> s;
 6         while(root || s.size() > 0) {
 7             if(root) {
 8                 s.push(root);
 9                 root = root->left;
10             }
11             else {
12                 root = s.top();
13                 s.pop();
14                 res.push_back(root->val);
15                 root = root->right;
16             }
17         }
18         return res;
19     }
20 };

View Code

postorder traversal比之前的两个要复杂了一些，但是为了使得三种traversal的形式上类似以方便记忆，我们使用了一个并不是最快的写法，当然复杂度上依然是O(n) time， O(n) space。这里使用一个pointer存储先前访问的节点，以避免重复访问右节点。

class Solution {
public:
    vector<int> postorderTraversal(TreeNode *root) {
        vector<int> res;
        stack<TreeNode *> s;
        TreeNode *pre = NULL;
        while(root || s.size() > 0) {
            if(root) {
                s.push(root);
                root = root->left;
            }
            else {
                root = s.top();
                if(root->right && root->right != pre)
                    root = root->right;
                else {
                    res.push_back(root->val);
                    s.pop();
                    pre = root;
                    root = NULL;
                }
            }
        }
        return res;
    }
};

View Code

postorder traversal还有一些更快的实现，大家可以参考https://leetcode.com/discuss/questions/oj/binary-tree-postorder-traversal 这个discuss里的解答以及http://www.programcreek.com/2012/12/leetcode-solution-of-iterative-binary-tree-postorder-traversal-in-java/ 和 http://www.geeksforgeeks.org/iterative-postorder-traversal/ 给出的方法。如果以后有机会，我再把这两个补充好，目前我得消化消化现在的实现。

接下来是level order traversal，本质上和BFS是一样的。在这里我使用queue保存节点，queue的front就是正在访问的节点，每次扩展当前节点就将他的子节点存入queue里，每一层结束的时候将一个NULL pointer放进queue里。这样每当queue的front是NULL的时候，我们知道当前的level结束了，所以事先要把root和一个NULL放入queue中。

 1 class Solution {
 2 public:
 3     vector<vector<int> > levelOrder(TreeNode *root) {
 4         vector<vector<int> > res;
 5         if(root == NULL)
 6             return res;
 7         vector<int> re;
 8         queue<TreeNode *> q;
 9         q.push(root);
10         q.push(NULL);
11         while(q.size() > 0) {
12             TreeNode *cur = q.front();
13             q.pop();
14             if(cur == NULL) {
15                 res.push_back(re);
16                 re.clear();
17                 if(q.size() > 0)
18                     q.push(NULL);
19             }
20             else {
21                 re.push_back(cur->val);
22                 if(cur->left)
23                     q.push(cur->left);
24                 if(cur->right)
25                     q.push(cur->right);
26             }
27         }
28         return res;
29     }
30 };

View Code

正如我们计划的，我们将介绍Morris traversal，这是一个使用O(n) time，O(1) space的算法，思路是使用空闲的指针来记下来访问的相关信息。

在学习的过程中，发现一篇博文讲解得非常非常清楚，在这里 http://www.cnblogs.com/AnnieKim/archive/2013/06/15/morristraversal.html 大家一定要读一读。

inorder traversal using Morris‘ algorithm

具体算法是这样的：

“1. 如果当前节点的左孩子为空，则输出当前节点并将其右孩子作为当前节点。

2. 如果当前节点的左孩子不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点。

a) 如果前驱节点的右孩子为空，将它的右孩子设置为当前节点。当前节点更新为当前节点的左孩子。

b) 如果前驱节点的右孩子为当前节点，将它的右孩子重新设为空（恢复树的形状）。输出当前节点。当前节点更新为当前节点的右孩子。

3. 重复以上1、2直到当前节点为空。” （摘自上述博文 http://www.cnblogs.com/AnnieKim/archive/2013/06/15/morristraversal.html）

 1 class Solution {
 2 public:
 3     vector<int> inorderTraversal(TreeNode *root) {
 4         vector<int> res;
 5         TreeNode *cur = root;
 6         while(cur) {
 7             if(!cur->left) {
 8                 res.push_back(cur->val);
 9                 cur = cur->right;
10             }
11             else {
12                 TreeNode *pre = cur->left;
13                 while(pre->right && pre->right != cur)
14                     pre = pre->right;
15                 if(pre->right == NULL) {
16                     pre->right = cur;
17                     cur = cur->left;
18                 }
19                 else {
20                     pre->right = NULL;
21                     res.push_back(cur->val);
22                     cur = cur->right;
23                 }
24             }
25         }
26         return res;
27     }
28 };

View Code

preorder traversal using Morris‘ algorithm

preorder的和inorder的几乎是完全一样的，区别只在于在什么地方返回。

 1 class Solution {
 2 public:
 3     vector<int> preorderTraversal(TreeNode *root) {
 4         TreeNode *cur = root;
 5         vector<int> res;
 6         while(cur) {
 7             if(!cur->left) {
 8                 res.push_back(cur->val);
 9                 cur = cur->right;
10             }
11             else {
12                 TreeNode *pre = cur->left;
13                 while(pre->right && pre->right != cur)
14                     pre = pre->right;
15                 if(pre->right == NULL) {
16                     res.push_back(cur->val); //only difference with inorder
17                     pre->right = cur;
18                     cur = cur->left;
19                 }
20                 else {
21                     pre->right = NULL;
22                     cur = cur->right;
23                 }
24             }
25         }
26         return res;
27     }
28 };

View Code

Balanced Binary Tree: https://leetcode.com/problems/balanced-binary-tree/

如前所述，tree的题基本都是traverse。有些题会需要特定的traverse，有些题不需要。这道题就无所谓用哪种了。这道题的难点是怎样一次遍历就既得到是否是balanced tree又得到当前的高度。方法是返回一个int值，当这个int值为负表示unbalanced subtree，为非负表示balanced subtree并且值是这个subtree的高度。这里用数字表示返回值传递多个信息的思路很值得注意。代码如下

 1 class Solution {
 2 public:
 3     bool isBalanced(TreeNode *root) {
 4         return helper(root) != -1;
 5     }
 6     
 7     int helper(TreeNode *root) {
 8         if(root == NULL)
 9             return 0;
10         int L = helper(root->left);
11         if(L == -1)
12             return -1;
13         int R = helper(root->right);
14         if(R == -1)
15             return -1;
16         return abs(L - R) <= 1 ? max(L, R) + 1: -1;
17     }
18 };

View Code

Symmetric Tree：https://leetcode.com/problems/symmetric-tree/

这道题有些绕，但仍然是基于traverse的，并且也无所谓使用哪种traverse的方式。但这道题需要仔细考虑好symmetric的条件

同时考虑一个节点的左右两个child：left， right。symmetric要满足：

1）left == null && right == null || left->val == right->val

2）left child of left and right child of right is symmetric && right child of left and left child of right is symmetric

recursive的代码如下

 1 class Solution {
 2 public:
 3     bool isSymmetric(TreeNode *root) {
 4         if(root == NULL)
 5             return true;
 6         return isSymmetric(root->left, root->right);
 7     }
 8     
 9     bool isSymmetric(TreeNode *lroot, TreeNode *rroot) {
10         if(lroot == NULL && rroot == NULL)
11             return true;
12         if(lroot == NULL || rroot == NULL)
13             return false;
14         if(lroot->val != rroot->val)
15             return false;
16         return isSymmetric(lroot->left, rroot->right) && isSymmetric(lroot->right, rroot->left);
17     }
18 };

View Code

如果使用iterative的写法的话，我这里使用的是level order traverse，与BFS是一样的。在这里我使用q保存节点，queue的front就是正在访问的节点，每次扩展当前节点就将他的子节点存入queue里，然后使用一个vector保存子节点层的数值，每访问完一层就检验一下这个vector是否是symmetric的，如果不是就return false。并且使用了一个dummy的TreeNode *来标记每一层的结束。具体代码如下：

 1 class Solution {
 2 public:
 3     bool isSymmetric(TreeNode *root) {
 4         if(root == NULL)
 5             return true;
 6         queue<TreeNode *> q;
 7         TreeNode *dummy;
 8         q.push(root);
 9         q.push(dummy);
10         vector<int> curlevel;
11         while(q.size() > 1) {
12             TreeNode *cur = q.front();
13             q.pop();
14             if(cur == dummy) {
15                 q.push(dummy);
16                 for(int i = 0; i < curlevel.size() / 2; i++) {
17                     if(curlevel[i] != curlevel[curlevel.size() - i - 1])
18                         return false;
19                 }
20                 curlevel.clear();
21             }
22             else {
23                 if(cur->left) {
24                     q.push(cur->left);
25                     curlevel.push_back(cur->left->val);
26                 }
27                 else {
28                     curlevel.push_back(INT_MIN);
29                 }
30                 if(cur->right) {
31                     q.push(cur->right);
32                     curlevel.push_back(cur->right->val);
33                 }
34                 else {
35                     curlevel.push_back(INT_MIN);
36                 }
37             }
38         }
39         return true;
40     }
41 };

View Code

Same Tree: https://leetcode.com/problems/same-tree/

这道题比较简单了。

 1 class Solution {
 2 public:
 3     bool isSameTree(TreeNode *p, TreeNode *q) {
 4         if(p == NULL && q == NULL)
 5             return true;
 6         if(p == NULL || q == NULL)
 7             return false;
 8         if(p->val != q->val)
 9             return false;
10         return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
11     }
12 };

View Code

Maximum Depth of Binary Tree: https://leetcode.com/problems/maximum-depth-of-binary-tree/

这道题应该算是leetcode中最简单的一道binary tree的题了。只要想清楚递归的关系就好。

1 class Solution {
2 public:
3     int maxDepth(TreeNode *root) {
4         if(root == NULL)
5             return 0;
6         return max(maxDepth(root->left), maxDepth(root->right)) + 1;
7     }
8 };

View Code

Unique Binary Search Tree: https://leetcode.com/problems/unique-binary-search-trees/

这道题是一道BST的题，并且用到了DP的方法。思路依然是找递归关系。我们知道BST的左子树和右子树依然是BST，于是递归关系就和这个有关了。我们依次让1...n的数字作为根，这样左子树和右子树就是两个以k1，k2，k1，k2 < n，为根的BST。而这两个问题我们在递归的过程中已经解决了。那么以当前的数字作为根的数量就是这两个子树的数量的乘积。用一个公式表达就是

技术分享

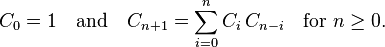
这其实是catalan数，具体详见wiki：http://en.wikipedia.org/wiki/Catalan_number

 1 class Solution {
 2 public:
 3     int numTrees(int n) {
 4         int num[n + 1] = {0};
 5         num[0] = 1;
 6         num[1] = 1;
 7         for(int i = 2; i < n + 1;i++) {
 8             for(int j = 0; j < i; j++) {
 9                 num[i] += num[j] * num[i - j - 1];
10             }
11         }
12         return num[n];
13     }
14 };

View Code

Unique Binary Search Tree II: https://leetcode.com/problems/unique-binary-search-trees-ii/

这道题和上一道是一样的思路，但是仔细想一下这个表达式不能用多项式表达，所以时间复杂度也就不能控制在多项式时间里了。

 1 class Solution {
 2 public:
 3     vector<TreeNode *> generateTrees(int n) {
 4         return helper(1, n);
 5     }
 6     
 7     vector<TreeNode *> helper(int start, int end) {
 8         vector<TreeNode *> res;
 9         if(start > end) {
10             res.push_back(NULL);
11             return res;
12         }
13         for(int k = start; k <= end; k++) {
14             vector<TreeNode *> leftTree = helper(start, k - 1);
15             vector<TreeNode *> rightTree = helper(k + 1, end);
16             for(vector<TreeNode *>::iterator lit = leftTree.begin(); lit != leftTree.end(); lit++) {
17                 for(vector<TreeNode *>::iterator rit = rightTree.begin(); rit != rightTree.end(); rit++) {
18                     TreeNode *T = new TreeNode(k);
19                     T->left = (*lit);
20                     T->right = (*rit);
21                     res.push_back(T);
22                 }
23             }
24         }
25         return res;
26     }
27 };

View Code

Recover Binary Search tree: https://leetcode.com/problems/recover-binary-search-tree/

这道题还蛮不好做的。首先我们发现BST按照inorder traversal得到的结果就是按顺序的，而且题目要求O(1) space，那肯定是morris traversal了。那么下一个问题就是怎样判断哪两个节点互换了。仔细观察，举几个例子会发现有两种情况，

1）相邻的两个互换了，那么在inorder traversal的结果里只出现一次相邻的某两个元素没有按递增顺序sorted，只要把这两个交换即可；

2）不相邻的两个互换了，那么inorder traversal的结果里会出现两次两个相邻的元素没有按递增顺序sorted，这是要注意了，其实被交换的是第一次出现时的大的那个数和第二次出现时的小的那个数，比如123456，1和4被交换的话，结果是423156，素以当我们发现423156时，第一次是42，第二次是31，我们要换的是4和1。

具体到算法实现中，我们始终记住inorder traversal的结果中当前节点的前驱节点，prev，以及两个指针temp1和temp2用于保存当前的可能互换的节点。一旦出现当前节点的值比前驱小，那么

1）如果是第一次出现这种情况，就分别保存当前节点在temp1和前驱节点在temp2；

2）如果是第二次出现，则将之前存储当时的当前节点的temp1存储成现在的当前节点。

于是找到了互换的两个节点。这样在inorder traversal结束之后，互换temp1和temp2的值就可以了。代码如下

 1 class Solution {
 2 public:
 3     void recoverTree(TreeNode *root) {
 4         TreeNode *cur = root;
 5         TreeNode *temp1 = NULL;
 6         TreeNode *temp2 = NULL;
 7         TreeNode *prev = NULL;
 8         while(cur) {
 9             if(!cur->left) {
10                 if(prev && cur->val < prev->val) {
11                     if(temp1)
12                         temp1 = cur;
13                     else {
14                         temp1 = cur;
15                         temp2 = prev;
16                     }
17                 }
18                 else
19                     prev = cur;
20                 cur = cur->right;
21             }
22             else {
23                 TreeNode *pre = cur->left;
24                 while(pre->right && pre->right != cur)
25                     pre = pre->right;
26                 if(pre->right == NULL) {
27                     pre->right = cur;
28                     cur = cur->left;
29                 }
30                 else {
31                     pre->right = NULL;
32                     if(prev && cur->val < prev->val) {
33                         if(temp1)
34                             temp1 = cur;
35                         else {
36                             temp1 = cur;
37                             temp2 = prev;
38                         }
39                     }
40                     else
41                         prev = cur;
42                     cur = cur->right;
43                 }
44             }
45         }
46         int temp = temp1->val;
47         temp1->val = temp2->val;
48         temp2->val = temp;
49     }
50 };

View Code

Populating Next Right Pointers in Each Node I: https://leetcode.com/problems/populating-next-right-pointers-in-each-node/

Populating Next Right Pointers in Each Node II: https://leetcode.com/problems/populating-next-right-pointers-in-each-node-ii/

这两道题乍一看可以用level order 来解决，但问题是题目要求用O(1) space，那就需要再进一步思考了。因为这道题的Tree的结构多定义了一个pointer指向当前节点后面的节点，当我们一层一层出的时候，刚好可以利用之前的结果来访问同一层中的下一个节点。这样只需要两个pointer指向下一层的第一个节点和当前层正在处理的节点就可以了。另外一个我做的时候感觉别扭的地方是怎样找到每次的第一个节点，思路上并不难，就是每层开始的时候先找到下一层的第一个节点，然后再继续一个节点一个节点的判断。

 1 /**
 2  * Definition for binary tree with next pointer.
 3  * struct TreeLinkNode {
 4  *  int val;
 5  *  TreeLinkNode *left, *right, *next;
 6  *  TreeLinkNode(int x) : val(x), left(NULL), right(NULL), next(NULL) {}
 7  * };
 8  */
 9 class Solution {
10 public:
11     void connect(TreeLinkNode *root) {
12         TreeLinkNode *cur = root;
13         TreeLinkNode *curnode = NULL;
14         while(root) {
15             cur = root;
16             curnode = NULL;
17             while(cur && !curnode) {
18                 if(cur->left)
19                     curnode = cur->left;
20                 else if(cur->right)
21                     curnode = cur->right;
22                 else
23                     cur = cur->next;
24             }
25             root = curnode;
26             while(cur) {
27                 if(curnode == cur->left && cur->right)
28                     curnode->next = cur->right;
29                 else if(curnode == cur->right)
30                     cur = cur->next;
31                 else {
32                     if(curnode != cur->left && cur->left)
33                         curnode->next = cur->left;
34                     else if(cur->right)
35                         curnode->next = cur->right;
36                     else
37                         cur = cur->next;
38                 }
39                 if(curnode->next)
40                     curnode = curnode->next;
41             }
42         }
43     }
44 };

View Code

Convert Sorted Array to Binary SearchTree：https://leetcode.com/problems/convert-sorted-array-to-binary-search-tree/

这道题用recursion，并不难做，要考虑到数组的中间的数就是BST的根节点，然后用递归（recursive）调用即可。

 1 class Solution {
 2 public:
 3     TreeNode *sortedArrayToBST(vector<int> &num) {
 4         return convert(num, 0, num.size() - 1);
 5     }
 6     
 7     TreeNode *convert(vector<int> &num, int start, int end) {
 8         if(start > end)
 9             return NULL;
10         int mid = (start + end) / 2;
11         TreeNode *root = new TreeNode(num[mid]);
12         root->left = convert(num, start, mid - 1);
13         root->right = convert(num, mid + 1, end);
14         return root;
15     }
16 };

View Code

与这道题类似的还有convert sorted list to binary search tree： https://leetcode.com/problems/convert-sorted-list-to-binary-search-tree/

思路一样，只是实现上有些不同。

 1 class Solution {
 2 public:
 3     TreeNode *sortedListToBST(ListNode *head) {
 4         ListNode *start = head;
 5         if(head == NULL)
 6             return NULL;
 7         while(head->next)
 8             head = head->next;
 9         ListNode *end = head;
10         return convert(start, end);
11     }
12     
13     TreeNode *convert(ListNode *start, ListNode *end) {
14         TreeNode *root = new TreeNode(0);
15         if(!start || !end || end->next == start) {
16             return NULL;
17         }
18         ListNode *slow = start;
19         ListNode *fast = start->next;
20         ListNode *preslow = NULL;
21         while(fast != end->next && fast) {
22             fast = fast->next;
23             if(fast != end->next && fast) {
24                 preslow = slow;
25                 fast = fast->next;
26                 slow = slow->next;
27             }
28         }
29         root->val = slow->val;
30         root->left = convert(start, preslow);
31         root->right = convert(slow->next, end);
32     }
33 };

View Code

Sum Root to Leaf Numbers: https://leetcode.com/problems/sum-root-to-leaf-numbers/

这道题其实并不难，但是要想明白递归的关系：就是每次访问节点的时候，他的父节点的sum值*10加上当前节点的值就是当前这个路径上的值。有几个细节的地方要考虑，怎么返回这个sum值，如果返回的不对，会出现重复计算，为了避免这个情况，我们在每个leaf节点的时候返回，而不是每次NULL的时候返回，这样避免了leaf节点重复计算。代码如下

 1 class Solution {
 2 public:
 3     int sumNumbers(TreeNode *root) {
 4         return helper(root, 0);
 5     }
 6     
 7     int helper(TreeNode *root, int sum) {
 8         if(root == NULL)
 9             return 0;
10         if(!root->right && !root->left)
11             return sum * 10 + root->val;
12         return helper(root->left, sum * 10 + root->val) + helper(root->right, sum * 10 + root->val);
13     }
14 };

View Code

还有一个比较讨巧但并不推荐的方法来传递和存储sum值，就是把当前路径上的sum值存在当前node的val里，但是会破坏tree的值，不很推荐。代码如下

 1 class Solution {
 2 public:
 3     int sumNumbers(TreeNode *root) {
 4         if(root == NULL)
 5             return 0;
 6         if(!root->right && !root->left)
 7             return root->val;
 8         if(root->right)
 9             root->right->val += root->val * 10;
10         if(root->left)
11             root->left->val += root->val * 10;
12         return sumNumbers(root->left) + sumNumbers(root->right);
13     }
14 };

View Code

Path Sum: https://leetcode.com/problems/path-sum/

这个题和上一个基本上是一个思路。

 1 class Solution {
 2 public:
 3     bool hasPathSum(TreeNode *root, int sum) {
 4         if(root == NULL)
 5             return false;
 6         if(!root->left && !root->right)
 7             return root->val == sum;
 8         return hasPathSum(root->right, sum - root->val) || hasPathSum(root->left, sum - root->val);
 9     }
10 };

View Code

Path Sum II: https://leetcode.com/problems/path-sum-ii/

这道题思路很清楚，就是用 dfs 遍历整个树，可以算是backtracking的基础模型了。

 1 class Solution {
 2 public:
 3     vector<vector<int>> pathSum(TreeNode* root, int sum) {
 4         vector<vector<int> > res; 
 5         vector<int> re;
 6         if(root)
 7             helper(root, sum, res, re);
 8         return res;
 9     }
10     
11     void helper(TreeNode* root, int sum, vector<vector<int> >& res, vector<int>& re) {
12         sum = sum - root->val;
13         re.push_back(root->val);
14         if(root->left == NULL && root->right == NULL && sum == 0) {
15             res.push_back(re);
16         }
17         else {
18             if(root->left) {
19                 helper(root->left, sum, res, re);
20                 re.pop_back();
21             }
22             if(root->right) {
23                 helper(root->right, sum, res, re);
24                 re.pop_back();
25             }
26         }
27     }
28 };

View Code

Minimum Depth of Binary Tree: https://leetcode.com/problems/minimum-depth-of-binary-tree/

博主表示这道题虽然被标为easy，但是一点也不easy啊。主要是要想明白这个min是有点特殊的，如果一个节点没有左或者右孩子，那么我们不能返回左或者右的minDepth的值，因为那一定是0，而我们并不认为这个的min是0，（否则就没有意义了啊）。

 1 int minDepth(TreeNode *root) {
 2         if(root == NULL)
 3             return 0;
 4         int leftmin = minDepth(root->left);
 5         int rightmin = minDepth(root->right);
 6         if(leftmin == 0)
 7             return rightmin + 1;
 8         if(rightmin == 0)
 9             return leftmin + 1;
10         return min(leftmin, rightmin) + 1;
11     }

View Code

Validate Binary Search Tree: https://leetcode.com/problems/validate-binary-search-tree/

这道题其实是要做一个inorder traversal。有一点改变的地方是在travers的时候返回值要随时存储当前的最大值。这个思路其实也可以改成是convert a BST into a sorted array / linkedList。

 1 class Solution {
 2 public:
 3     bool isValidBST(TreeNode *root) {
 4         if(root == NULL || (root->left == NULL && root->right == NULL))
 5             return true;
 6         long max = LONG_MIN;
 7         return helper(root, max);
 8     }
 9     
10     bool helper(TreeNode *root, long& max) {
11         bool isLeft = true, isRight = true, isBST = true;
12         if(root->left)
13             isLeft = helper(root->left, max);
14         if(max < root->val)
15             max = root->val;
16         else
17             isBST = false;
18         if(isLeft && isBST && root->right)
19             isRight = helper(root->right, max);
20         return isLeft && isRight && isBST;
21     }
22 };

View Code

Binary Tree Zigzag Level Order Traversal: https://leetcode.com/problems/binary-tree-zigzag-level-order-traversal/

这道题就是把 level order traversal 改动一下，思路一致。

 1 class Solution {
 2 public:
 3     vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
 4         queue<TreeNode*> q;
 5         vector<vector<int> > res;
 6         vector<int> re;
 7         if(root == NULL)
 8             return res;
 9         q.push(root);
10         q.push(NULL);
11         bool odd = true;
12         while(q.size() > 0) {
13             TreeNode* cur = q.front();
14             q.pop();
15             if(cur) {
16                 re.push_back(cur->val);
17                 if(cur->left)
18                     q.push(cur->left);
19                 if(cur->right)
20                     q.push(cur->right);
21             }
22             else {
23                 if(q.size() > 0)
24                     q.push(NULL);
25                 if(odd)
26                     res.push_back(re);
27                 else {
28                     reverse(re.begin(), re.end());
29                     res.push_back(re);
30                 }
31                 re.clear();
32                 odd = !odd;
33             }
34         }
35         return res;
36     }
37 };

View Code

Construct Binary Tree from Inorder and Postorder Traversal: https://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/

Construct Binary Tree from Inorder and preorder Traversal: https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/

这两道题主要帮助我们想明白inorder，preorder和postorder之间的关联，举几个例子并不难看出。需要注意的是为了降低时间复杂度，我们只传当前考虑的index，这样就涉及到了计算index的问题，楼主就是在这个问题上卡了一下，导致不能一遍通过。

 1 class Solution {
 2 public:
 3     TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder) {
 4         if(inorder.size() == 0)
 5             return NULL;
 6         return helper(inorder, postorder, 0, inorder.size() - 1, 0, postorder.size() - 1);
 7     }
 8     
 9     TreeNode *helper(vector<int> &inorder, vector<int> &postorder, int instart, int inend, int poststart, int postend) {
10         if(instart > inend || poststart > postend)
11             return NULL;
12         int rootval = postorder[postend--];
13         int breakpoint = 0;
14         for(int i = instart; i <= inend; i++) {
15             if(inorder[i] == rootval) {
16                 breakpoint = i;
17                 break;
18             }
19         }
20         int leftsize = breakpoint - instart;
21         int rightsize = inend - breakpoint;
22         TreeNode *root = new TreeNode(rootval);
23         root->left = helper(inorder, postorder, instart, breakpoint - 1, poststart, poststart + leftsize - 1);
24         root->right = helper(inorder, postorder, breakpoint + 1, inend, poststart + leftsize , postend);
25         return root;
26     }
27 };

View Code

 1 class Solution {
 2 public:
 3     TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
 4         if(inorder.size() == 0)
 5             return NULL;
 6         return buildTree(preorder, inorder, 0, inorder.size() - 1, 0, inorder.size() - 1);
 7     }
 8     
 9     TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder, int prestart, int preend, int instart, int inend) {
10         if(prestart > preend || instart > inend)
11             return NULL;
12         int rootval = preorder[prestart];
13         TreeNode* tn = new TreeNode(rootval);
14         int breakpoint = instart;
15         for(; breakpoint <= inend; breakpoint++) {
16             if(inorder[breakpoint] == rootval)
17                 break;
18         }
19         tn->left = buildTree(preorder, inorder, prestart + 1, prestart + breakpoint - instart, instart, breakpoint - 1);
20         tn->right = buildTree(preorder, inorder, prestart + breakpoint - instart + 1, preend, breakpoint + 1, inend);
21         return tn;
22     }
23 };

View Code

binary tree/tree相关问题 review

标签：

原文地址：http://www.cnblogs.com/walcottking/p/4436461.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行