标签:
题意:在一个正方形内画n个M,求最多能分成多少个平面
sol:这种求划分成多少个平面的题第一反应肯定是欧拉公式:
二维平面上的欧拉公式:V+F-E=1 (V:Vertices,F:Faces,E:Edges)
然后我们画出三个M的情况看一下:(果然Pad是个画图神器。。去年网赛的时候光画图就画了半天。。。)
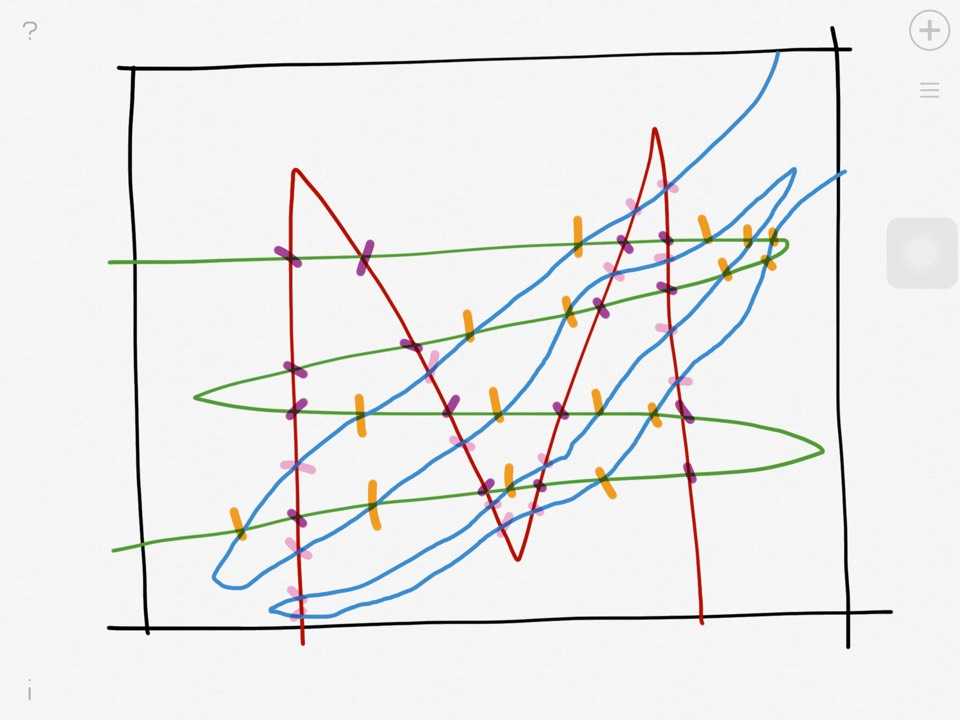
最多的情况就是每两个M都相交
先分析vertices:两个M相交共16个交点,再加上每个M和正方形相交又有2个交点。
所以加起来就是V=16*C(n,2)+2*n=8*n*n-6n
再来看edges:先不考虑每个M末端被封死的那3个角,一个M上4个边,
对于每个边,每和1个M相交就会多4个边。如果有n个M,每条边就会和n-1个M相交,变成4*(n-1)+1条边。n个M上4n个边就是[4*(n-1)+1]*4n
再处理封死的角,-3n
再加上和正方形相交产生的边,+2n
加起来就是E=[4(n-1)+1]*4n-3n+2n
最后计算得F=8*n*n-7n+1
标签:
原文地址:http://www.cnblogs.com/pdev/p/4536843.html