POJ 2635-The Embarrassed Cryptographer(高精度求模+同余模定理)

标签：高精度求模   同余模定理   数论   

Appoint description:  System Crawler  (2015-05-28)

Description

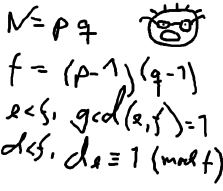The young and very promising cryptographer Odd Even has implemented the security module of a large system with thousands of users, which is now in use in his company. The cryptographic keys are created from the product of two primes, and are believed to be secure because there is no known method for factoring such a product effectively. 
What Odd Even did not think of, was that both factors in a key should be large, not just their product. It is now possible that some of the users of the system have weak keys. In a desperate attempt not to be fired, Odd Even secretly goes through all the users keys, to check if they are strong enough. He uses his very poweful Atari, and is especially careful when checking his boss‘ key.

Input

The input consists of no more than 20 test cases. Each test case is a line with the integers 4 <= K <= 10 ¹⁰⁰ and 2 <= L <= 10 ⁶. K is the key itself, a product of two primes. L is the wanted minimum size of the factors in the key. The input set is terminated by a case where K = 0 and L = 0.

Output

For each number K, if one of its factors are strictly less than the required L, your program should output "BAD p", where p is the smallest factor in K. Otherwise, it should output "GOOD". Cases should be separated by a line-break.

Sample Input

143 10
143 20
667 20
667 30
2573 30
2573 40
0 0

Sample Output

GOOD
BAD 11
GOOD
BAD 23
GOOD
BAD 31

题意：给定一个大数str，str是两个大素数的乘积的值，再给定一个int内的数n，问这两个大素数中最小的一个是否小于n，如果小于则输出GOOD，否则输出BAD和两个素数中最小的。

思路：先用素数筛把小于1100000的素数都找出来。然后把str转化为一堆千进制。对于每一个千进制，把i从2到n遍历一遍即可。

PS：然而学习了一下高精度求模，原来可以这么搞，Orz。

然而中学生的高精度取模也是醉了点击打开链接

高精度求模。

主要利用qk数组和同余模定理。
例如要验证123是否被3整除，只需求模124%3
但当123是一个大数时，就不能直接求，只能通过同余模定理对大数“分块”间接求模
具体做法是：
先求1%3 = 1
再求（1*10+2）%3 = 0
再求 （0*10+4）% 3 = 1
那么就间接得到124%3=1，这是显然正确的
而且不难发现， （1*10+2）*10+4 = 124
这是在10进制下的做法，千进制也同理，*10改为*1000就可以了。

#include <stdio.h>
#include <math.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <sstream>
#include <algorithm>
#include <set>
#include <queue>
#include <stack>
#include <map>
using namespace std;
typedef long long LL;
const int inf=0x3f3f3f3f;
const double eps=1e-10;
const double pi= acos(-1.0);
const int MAXN=1e6+10;
int prime[MAXN]={2,3,5};
int qk[1010];
//素数筛
void is_prime()
{
    int i,j;
    int flag=0;
    int gcd=2;
    int k=3;
    for(i=7;i<MAXN;i+=gcd){
        flag=0;
        gcd=6-gcd;
        for(j=0;prime[j]*prime[j]<=i;j++){
            if(i%prime[j]==0){
                flag=1;
                break;
            }
        }
        if(!flag)
            prime[k++]=i;
    }
}
//高精度K对p求模，因数检查(整除)
int mod(int *K,int m,int len)
{
   int res=0;
   for(int i=len-1;i>=0;i--)//千进制K是逆序存放，因为计算起来方便
    res=(res*1000+K[i])%m; //同余模定理
   if(!res) return 0; //K被整除 
   else  return 1;
}

int main()
{
    char str[1010];
    int n,i,j;
    int flag;
    is_prime();
    while(~scanf("%s %d",str,&n)){
        if(str[0]=='0'&&n==0) break;
        memset(qk,0,sizeof(qk));
        int len=strlen(str);
        int ii=0;
        for(int i=len-1;i>=0;i-=3){//把str转换为千进制qk，其中qk局部顺序，全局倒序 
                                   //如str=1234567=[  1][234][567] ，则qk=[567][234][1  ]  
            if(i>=2)
            qk[ii]=(str[i]-'0')+(str[i-1]-'0')*10+(str[i-2]-'0')*100;
            else if(i==1)
            qk[ii]=(str[i]-'0')+(str[i-1]-'0')*10;
            else if(i==0)
            qk[ii]=(str[i]-'0');
            ii++;
        }
        int len_qk=(len+2)/3;
        int qMin=0;//能整除qk且比n小的在prime中的最小素数下标
        flag=1;
        while(prime[qMin]<n){//枚举prime中比L小的素数  
            if(!mod(qk,prime[qMin],len_qk)){
                flag=0;
                printf("BAD %d\n",prime[qMin]);
                break;
            }
            qMin++;
        }
        if(flag)
            puts("GOOD");
    }
    return 0;
}

POJ 2635-The Embarrassed Cryptographer(高精度求模+同余模定理)

标签：高精度求模   同余模定理   数论   

原文地址：http://blog.csdn.net/u013486414/article/details/46129453