标签:codeforces
比赛链接:http://codeforces.com/contest/437
Once upon a time a child got a test consisting of multiple-choice questions as homework. A multiple-choice question consists of four choices: A, B, C and D. Each choice has a description, and the child should find out the only one that is correct.
Fortunately the child knows how to solve such complicated test. The child will follow the algorithm:
You are given a multiple-choice questions, can you predict child‘s choose?
The first line starts with "A." (without quotes), then followed the description of choice A. The next three lines contains the descriptions of the other choices in the same format. They are given in order: B, C, D. Please note, that the description goes after prefix "X.", so the prefix mustn‘t be counted in description‘s length.
Each description is non-empty and consists of at most 100 characters. Each character can be either uppercase English letter or lowercase English letter, or "_".
Print a single line with the child‘s choice: "A", "B", "C" or "D" (without quotes).
A.VFleaKing_is_the_author_of_this_problem
B.Picks_is_the_author_of_this_problem
C.Picking_is_the_author_of_this_problem
D.Ftiasch_is_cute
D
A.ab
B.abcde
C.ab
D.abc
C
A.c
B.cc
C.c
D.c
B
In the first sample, the first choice has length 39, the second one has length 35, the third one has length 37, and the last one has length 15. The choice D (length 15) is twice shorter than all other choices‘, so it is great choice. There is no other great choices so the child will choose D.
In the second sample, no choice is great, so the child will choose the luckiest choice C.
In the third sample, the choice B (length 2) is twice longer than all other choices‘, so it is great choice. There is no other great choices so the child will choose B.
题目大意:一些题目,若有一个选项长度为其他的两倍及以上或者为其他的二分之一及以下则它是目标选项,若只有一个目标选项则输出否则输出C
题目分析:直接枚举模拟
#include <cstdio>
#include <string>
#include <iostream>
using namespace std;
int main()
{
string s[4];
cin >> s[0] >> s[1] >> s[2] >> s[3];
int l1 = s[0].length() - 2;
int l2 = s[1].length() - 2;
int l3 = s[2].length() - 2;
int l4 = s[3].length() - 2;
bool flag = true;
int cnt = 0;
char ans;
if(2 * l1 <= l2 && 2 * l1 <= l3 && 2 * l1 <= l4)
{
cnt ++;
ans = 'A';
}
if(l1 >= 2 * l2 && l1 >= 2 * l3 && l1 >= 2 * l4)
{
cnt ++;
ans = 'A';
}
if(2 * l2 <= l1 && 2 * l2 <= l3 && 2 * l2 <= l4)
{
cnt ++;
ans = 'B';
}
if(l2 >= 2 * l1 && l2 >= 2 * l3 && l2 >= 2 * l4)
{
cnt ++;
ans = 'B';
}
if(2 * l4 <= l1 && 2 * l4 <= l2 && 2 * l4 <= l3)
{
cnt ++;
ans = 'D';
}
if(l4 >= 2 * l1 && l4 >= 2 * l2 && l4 >= 2 * l3)
{
cnt ++;
ans = 'D';
}
if(2 * l3 <= l1 && 2 * l3 <= l2 && 2 * l3 <= l4)
{
cnt ++;
ans = 'C';
}
if(l3 >= 2 * l1 && l3 >= 2 * l2 && l3 >= 2 * l4)
{
cnt ++;
ans = 'C';
}
if(cnt > 1 || cnt == 0)
printf("C\n");
else
printf("%c\n", ans);
}
At the children‘s day, the child came to Picks‘s house, and messed his house up. Picks was angry at him. A lot of important things were lost, in particular the favorite set of Picks.
Fortunately, Picks remembers something about his set S:
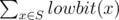 was equal to
sum; here lowbit(x) equals
2k where
k is the position of the first one in the binary representation of
x. For example, lowbit(100102)?=?102,?lowbit(100012)?=?12,?lowbit(100002)?=?100002
(binary representation).
was equal to
sum; here lowbit(x) equals
2k where
k is the position of the first one in the binary representation of
x. For example, lowbit(100102)?=?102,?lowbit(100012)?=?12,?lowbit(100002)?=?100002
(binary representation). Can you help Picks and find any set S, that satisfies all the above conditions?
The first line contains two integers: sum,?limit (1?≤?sum,?limit?≤?105).
In the first line print an integer n (1?≤?n?≤?105), denoting the size of S. Then print the elements of set S in any order. If there are multiple answers, print any of them.
If it‘s impossible to find a suitable set, print -1.
5 5
2 4 5
4 3
3 2 3 1
5 1
-1
In sample test 1: lowbit(4)?=?4,?lowbit(5)?=?1,?4?+?1?=?5.
In sample test 2: lowbit(1)?=?1,?lowbit(2)?=?2,?lowbit(3)?=?1,?1?+?2?+?1?=?4.
题目大意:从1到limit中选一些数字让他们lowbit()以后的值相加等于sum
题目分析:先预处理lowbit的值,然后贪心,从大的开始选,理由是大的灵活度比较低
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define ll long long
using namespace std;
int const MAX = 1e5 + 2;
struct DATA
{
int idx, val;
}a[MAX];
int sum, lim, n;
bool has[MAX];
int ans[MAX];
int lowbit(int x)
{
return x & (-x);
}
bool cmp(DATA a, DATA b)
{
return a.val > b.val;
}
void pre()
{
for(int i = 1; i <= lim; i++)
{
a[i].val = lowbit(i);
a[i].idx = i;
}
sort(a + 1, a + lim + 1, cmp);
}
int find(int x)
{
for(int i = 1; i <= lim; i++)
{
if(!has[i] && a[i].val <= x)
{
has[i] = true;
return i;
}
}
return -1;
}
int main()
{
scanf("%d %d", &sum, &lim);
pre();
bool flag = false;
int cnt = 0, idx;
memset(has, false, sizeof(has));
while(!flag)
{
if(sum == 0)
{
flag = true;
break;
}
int idx = find(sum);
if(idx == -1)
break;
ans[cnt ++] = a[idx].idx;
sum -= a[idx].val;
}
if(!flag)
printf("-1\n");
else
{
printf("%d\n", cnt);
for(int i = 0; i < cnt - 1; i++)
printf("%d ", ans[i]);
printf("%d\n", ans[cnt - 1]);
}
}
On Children‘s Day, the child got a toy from Delayyy as a present. However, the child is so naughty that he can‘t wait to destroy the toy.
The toy consists of n parts and m ropes. Each rope links two parts, but every pair of parts is linked by at most one rope. To split the toy, the child must remove all its parts. The child can remove a single part at a time, and each remove consume an energy. Let‘s define an energy value of part i as vi. The child spend vf1?+?vf2?+?...?+?vfk energy for removing part i where f1,?f2,?...,?fk are the parts that are directly connected to the i-th and haven‘t been removed.
Help the child to find out, what is the minimum total energy he should spend to remove all n parts.
The first line contains two integers n and m (1?≤?n?≤?1000; 0?≤?m?≤?2000). The second line contains n integers: v1,?v2,?...,?vn (0?≤?vi?≤?105). Then followed m lines, each line contains two integers xi and yi, representing a rope from part xi to part yi (1?≤?xi,?yi?≤?n; xi?≠?yi).
Consider all the parts are numbered from 1 to n.
Output the minimum total energy the child should spend to remove all n parts of the toy.
4 3 10 20 30 40 1 4 1 2 2 3
40
4 4 100 100 100 100 1 2 2 3 2 4 3 4
400
7 10 40 10 20 10 20 80 40 1 5 4 7 4 5 5 2 5 7 6 4 1 6 1 3 4 3 1 4
160
One of the optimal sequence of actions in the first sample is:
So the total energy the child paid is 20?+?10?+?10?+?0?=?40, which is the minimum.
In the second sample, the child will spend 400 no matter in what order he will remove the parts.
题目大意:删除一个图上所有的边,每次删除的代价为边上两点权值较小的那个,求全部删除后的最小代价
题目分析:不管按什么顺序,每个边对应的代价都是固定的,所以直接按边的输入顺序把每条边的代价加起来就可以了。。。居然放在C题。。。
#include <cstdio>
#include <algorithm>
using namespace std;
int n, m;
int a[2005];
int main()
{
int ans = 0;
scanf("%d %d", &n, &m);
for(int i = 1; i <= n; i++)
scanf("%d", &a[i]);
while(m--)
{
int x, y;
scanf("%d %d", &x, &y);
ans += min(a[x], a[y]) ;
}
printf("%d\n", ans);
}
Of course our child likes walking in a zoo. The zoo has n areas, that are numbered from 1 to n. The i-th area contains ai animals in it. Also there are m roads in the zoo, and each road connects two distinct areas. Naturally the zoo is connected, so you can reach any area of the zoo from any other area using the roads.
Our child is very smart. Imagine the child want to go from area p to area q. Firstly he considers all the simple routes from p to q. For each route the child writes down the number, that is equal to the minimum number of animals among the route areas. Let‘s denote the largest of the written numbers as f(p,?q). Finally, the child chooses one of the routes for which he writes down the value f(p,?q).
After the child has visited the zoo, he thinks about the question: what is the average value of f(p,?q) for all pairs p,?q (p?≠?q)? Can you answer his question?
The first line contains two integers n and m (2?≤?n?≤?105; 0?≤?m?≤?105). The second line contains n integers: a1,?a2,?...,?an (0?≤?ai?≤?105). Then follow m lines, each line contains two integers xi and yi (1?≤?xi,?yi?≤?n; xi?≠?yi), denoting the road between areas xi and yi.
All roads are bidirectional, each pair of areas is connected by at most one road.
Output a real number — the value of 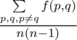 .
.
The answer will be considered correct if its relative or absolute error doesn‘t exceed 10?-?4.
4 3 10 20 30 40 1 3 2 3 4 3
16.666667
3 3 10 20 30 1 2 2 3 3 1
13.333333
7 8 40 20 10 30 20 50 40 1 2 2 3 3 4 4 5 5 6 6 7 1 4 5 7
18.571429
Consider the first sample. There are 12 possible situations:
Another 6 cases are symmetrical to the above. The average is
 .
.
Consider the second sample. There are 6 possible situations:
Another 3 cases are symmetrical to the above. The average is
 .
.
题目大意:n个点每个都有一个权值,被m条边相连每条边的权值就等于两个端点中那个小的,保证图是连通的,求所有的f(p, q)之和除以n*(n-1).p, q为任意两个点,f(p, q)就为p到q边上遇到的包括p, q在内的权值最小的点
题目分析:贪心加并查集,从大边开始,如果两个端点不在一个集合则合并,且这次边产生的影响次数用乘法原理可以得到为 cnt[r1]*cnt[r2],因为是降序的,已合并的点全都是经历了更长的边,所以用乘法原理,当前两个端点所在集合的个数互乘一下,便是此刻的边产生的影响次数。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int const MAX = 1e5 + 5;
struct EDGE
{
int u, v, w;
}e[MAX];
int n, m;
int fa[MAX], cnt[MAX], val[MAX];
double ans;
bool cmp(EDGE a, EDGE b)
{
return a.w > b.w;
}
void UF_set()
{
for(int i = 1; i <= n; i++)
{
fa[i] = i;
cnt[i] = 1;
}
}
int Find (int x)
{
return x == fa[x] ? x : fa[x] = Find(fa[x]);
}
void Union(int a, int b, int val)
{
int r1 = Find(a);
int r2 = Find(b);
if(r1 != r2)
{
ans += (double) val * cnt[r1] * cnt[r2];
cnt[r1] += cnt[r2];
fa[r2] = r1;
}
}
int main ()
{
ans = 0;
scanf("%d %d", &n, &m);
UF_set();
for(int i = 1; i <= n; i++)
scanf("%d", &val[i]);
for(int i = 0; i < m; i++)
{
scanf("%d %d", &e[i].u, &e[i].v);
e[i].w = min(val[e[i].u], val[e[i].v]);
}
sort(e, e + m, cmp);
for(int i = 0; i < m; i++)
Union(e[i].u, e[i].v, e[i].w);
printf("%.6lf\n", ans * 2.0 / (1.0 * n * (n - 1)));
}
Codeforces Round #250 (Div. 2) (ABCD题解)
标签:codeforces
原文地址:http://blog.csdn.net/tc_to_top/article/details/46325555