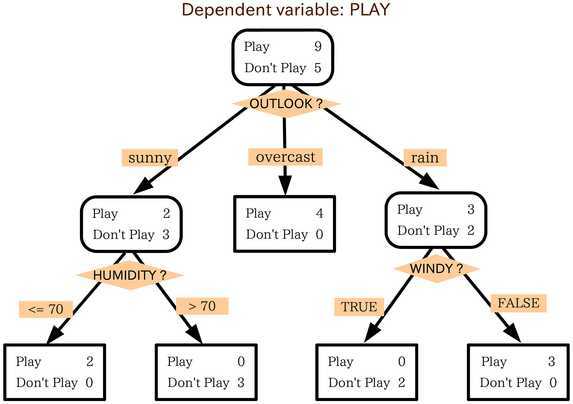
 ?
? 可见,决策树上的判断节点是对某一个属性进行判断,生成的路径数量为该属性可能的取值,最终到叶子节点时,就完成一个分类(或预测)。决策树具有直观、易于解释的特性。
2、决策树生成算法
?本文主要讨论如何由一个给定的训练集生成一个决策树。如果都一个数据集合$D$,其特征集合为$A$,那么以何种顺序对A中的特征进行判断就成为决策树生成过程中的关键。首先给出一个决策树生成算法-ID3算法(参考《统计学习方法》李航著)
--------------------我是算法开始分割线-------------------------------------------
ID3算法:
输入:训练数据集D,特征集A,阈值e
输出:决策树T
(1)若D中所有样本属于同一类Ck,则T为单节点树,并将类Ck作为该节点的类标记,返回T;
(2)A为空集,T为单节点树,将D中实例数最大的类Ck作为该节点的类标记,返回T;
(3)否则,计算A中各特征对D的信息增益,选择信息增益最大的特征值Ag;
(4)如果Ag<e,则置T为单节点树,将D中实例数最大的类Ck作为该节点的类标记,返回T;
(5)否则,对Ag的每一个可能的取值ai,依Ag=ai将D分割为若干非空子集Di,将Di中实例数最大的类作为标记,构建子节点,由节点及其子节点构成树T,返回T;
(6)对第i个子节点,以Di为训练集,以 A-{Ag}为特征集,递归调用(1)~(5)步,得到子树Ti,返回Ti。
--------------------我是算法结束分割线-------------------------------------------
算法第(3)步中,信息增益是评估每一个特征值对D的划分效果,划分的原则为将无序的数据变得尽量有序。评价随机变量不确定性的一个概念是熵,熵越大,不确定性越大。如果确定一个特征Ag,在确定该特征前后,D的熵的变化值就是特征Ag的信息增益。
3、熵及信息增益
熵:
设X是一个取有限个值(n)的离散随机变量,其概率分布为
\[P(X=x_{i})=P_{i}, i=1,2,...,n\]
则随机变量X的熵定义为
\[H(x) = - \sum\limits_{i = 1}^n {{P_i}\log {P_i}} \]
信息增益:
训练集为\(D\),\(|D|\)为样本容量,设有k个类\({C_k}\),k=1,...k, \({|C_k|}\)为类\({C_k}\)的样本个数,且有\(\sum\limits_{i = 1}^k {|{C_k}|} = |D|\)
设特征A有n个不同取值\(\{ {a_{1,}}{a_2}, \cdots ,{a_n}\} \) ,根据A的值,将D划分为n个子集\({D_1},{D_2}, \cdots ,{D_n}\), \({|D_i|}\)为\({D_i}\) 的样本数,\(\sum\limits_{i = 1}^n {|{D_i}|} = |D|\)。
记子集\({D_i}\)中属于类\({C_k}\)的样本集合为\({D_{ik}}\),即\({D_{ik}} = {D_i} \cap {C_k}\)。
\({|D_{ik}|}\)为\({D_{ik}}\)的样本个数。
(1)数据集D的经验熵H(D)
\[H(D) = - \sum\limits_{k = 1}^K {\frac{{|{C_k}|}}{{|D|}}{{\log }_2}} \frac{{|{C_k}|}}{{|D|}}\]
(2)特征A对数据集D的经验条件熵H(D|A)
\[H(D|A) = \sum\limits_{i = 1}^n {\frac{{|{D_i}|}}{{|D|}}H({D_i}) = - } \sum\limits_{i = 1}^n {\frac{{|{D_i}|}}{{|D|}}\sum\limits_{k = 1}^K {\frac{{|{D_{ik}}|}}{{|{D_i}|}}} } {\log _2}\frac{{|{D_{ik}}|}}{{|{D_i}|}}\]
(3)计算信息增益
\[g(D,A) = H(D) - H(D|A)\]
信息增益越大,表示A对D趋于有序的贡献越大。
 ?
?